поворота объекта отнсительно той же системы координат - курс К, дифферент и крен 6. Пусть требуется сохранять неизменным направление на визируемую точку при перемещениях подвижного объекта.

Возьмем единичный вектор, направленный в точку визирования, и спроектируем его на оси горизонтной системы

Зенит

Ттиаизиробанш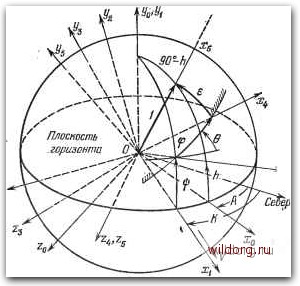

Рис. 1.4. К задаче стабилизащш визирующего устройства на подвижном объекте.

координат Oxij/iZi. Затем повернем эту систему координат последовательно на углы диф(юрента ij), крена 6, углы поворота оси визирующего устройства ф и е. В результате этих поворотов система координат Оху будет так расположена, что ось ОХй совпадает с единичным вектором, а оси Ог/5 и Ozb будут ему перпендикулярны. При этом проекция единичного вектора на ось Ох будет равна единице, а на две другие оси - нулю. Условия г/5 = О и = О служат признаком того, что углы поворота ф и е реализованы правильно и визирующее устройство направлено в заданную точку небесной сферы.

Формулы преобразования координат в соответствии с некоторым поворотом системы координат Oxyz относительно оси Oz на угол а (рис. 1.Б) имеют вид

ж" = д; cos а + у sin а, у = у cos (

>a + sina, » > а - л; sin а. J

(1.1)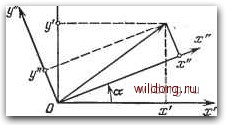

Рис. 1.Б. Задача преобразования координат.

Пересчет координат по формулам (1.1) делается так называемым преобразователем координат, в качестве которого может использоваться ЦВМ. Для реализации последовательных поворо-тов на углы ft, К - А, - У ф, 6, ф и е требуется шесть преобразователей координат. Схема такого вычислительного устройства, реализуемого на ЦВМ, изображена на рис. 1.6. Углы, на которые последовательно осуществляется поворот исходного единичного вектора, должны вводиться в ЦВМ от соответствующих кодирующих датчиков углов, соединенных с осями гироскопического стабилизатора, вырабатывающего углы (К - ). ф и 6, и с осями приводов наведения по углам ф и е. Выходные сигналы г/5 = Ае и 26 = Аф подаются на входы приводов наведения.

Нетрудно видеть, что с точки зрения динамики системы управления ЦВМ выполняет функции сравнивающего устройства, определяющего разности Аф и Ае. Однако эти разности определяются в результате проведения значительного объема вычислений.

Следует заметить, что, вообще говоря, углы Л и ft являются функциями времени. Поэтому в действительности для визирования определенной точки небесной сферы требуется задать координаты этой точки в системе координат, связанной с небесной сферой, например склонение и часовой угол, а затем преобразовать эти координаты в географическую систему координат, что требует реализации в ЦВМ еще двух дополнитель.ных.ишш!казй]Ши координат.

Вторая, наиболее часто возлагаемая на ЦВМ задача, заключается в обеспечении желаемых динамических характеристик системы управления посредством использования корректирующих программ в ЦВМ. В этом случае ЦВМ представляет собой по существу цифровой фильтр

с заданньши характери-

=sin Л

стиками.

В качестве примера рассмотрим систему стабилизации космического корабля «Апполон»[ 121]. В случае совместного полета корабля вместе с лунным отсеком возможны два режима. Первый режим соответствует номинальным условиям заполнения топливных баков и носит название широкополосного режима. Частотные характеристики разомкнутой системы управления для этого режима изображены на рис. 1.7, а. Кривая I соответствует случаю учета контура компенсации эксцентриситета вектора тяги, а кривые 2 - контурам наведения и компенсации эксцентриситета вектора тяги. Основная частота среза равна 1,25 рад/с. Корректирующий фильтр вносит стабилизацию на частотах упругих тонов, меньших 8,4 рад/с, за счет фазового запаздывания. При этом запас устойчивости по фазе на резонансной частоте составляет 35°. В широкополосном режиме обеспечивается стабилизация на любых жидкостных тонах, присущих кораблю с лунным отсеком в случае полного или почти полного заполнения взлетных и посадочных баков лунной кабины.

Однако при частичном заполнении топливных баков лунной кабины н почти цолном опорожнении топливных

5 =

Рис. 1.6. Структура преобразователя координат.