Из последнего выражения следует, что квантование по уровню расширяет спектр входного сигнала тем сильнее, чем больше отношение ao/6i. Однако при больших значениях отношения 0-0/61 формула (3.162) перестает быть справедливой, так как оказывается неправильным разложение (3.158).

Спектральная плотность для дискретного случая (при учете квантования по времени) может быть получена из (3.163) на основании приведенной выше формулы (3.59). Используя ее, имеем

(3.164)

где эквивалентная постоянная времени

-cth

(3.165)

Если ограничиться учетом только первой составляющей бесконечной суммы (3.164) и ввести корректирующий множитель с тем, чтобы интеграл по всем частотам от спектральной плотности давал бы дисперсию, то вместо (3.164) получим

6. 27-3 14

6! Л

(3.166)

(3.167)

Для случая 00 61 приходится искать другие пути определения спектральной плотности шумовой ошибки квантования. Один из возможных способов заключается в следующем.

Изобразим функцию р2(т) в виде графика (рис. 3.14) для случая п=\. При известной нормированной корреляционной функции входного сигнала р(т) это можно сделать по формуле (3.155). Построенный график дает

возможность подобрать некоторую аппроксимацию функции Ра (т), удобную для последующего использования.

Наиболее грубая аппроксимация получается при использовании прямоугольника с высотой, равной единице,

и протяженностью, равной времени корреляции

Тк = 5р2(т)т. (3.168)

Можно использовать параболическую или иную зависимость. Все они в той или иной мере приводят к цели. С точки зрения последующего использования наиболее удобна аппроксимация графика Рг (т) отрезком косину-сорщы Ра (т) cos (diT, рассматриваемой в интервале - TiT<Ti, где Ti определяется из условия (OiTi = 0,5n. Так как площадь этого отрезка косинусоиды для положительных значений т равна 2tiK""1, то время Ti и частота «1 могут быть определены из времени корреляции: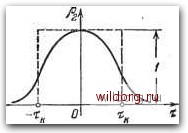

Рис. 3.14. Аппроксимация коэффициента корреляции.

Ti=-

(3.169)

Аналогичным образом для r>1 можно ввести аппроксимирующую функцию cos(d„t. Значение угловой частоты определяется временем корреляции при выбранном значении п.

Наиболее вероятен случай, когда справедливы соотношения

(3.170)

Однако окончательное решение этого вопроса может быть сделано только пссле исследования для заданного вида функции р(т). В результате подобной аппроксима-

ции функция (3.154) приобретает вид

со п = 1

(3.171)

формула (3.171) позволяет в простейших случаях задания р(т) найти спектральную плотность шума квантования для ao>6i- Пусть, например, корреляцрюнная функция входного сигнала определяется (3.161). Тогда формула (3.171) может быть записана следующим образом:

п = 1

(l-p(T))]cosco„T (3.172)

при I т I я/2«)„ = т„. Далее, можно разложить функцию р(т) в ряд, учитывая то обстоятельство, что существование ее для времени т>т„ не имеет значения, так как при этом coscu„TsO. Ограничиваясь поэтому линейным членом разложения, имеем

2 -тр

COS Сй„Т.

(3.173)

Применение преобразования Фурье к корреляционной функции (3.173) дает спектральную плотносгь шума квантования по уровню

(ю) 2

п«<1

2ца?

(3.174)

Спектральная плотность представляет совокупность отдельных составляющих, каждая из которых содержит два пика на частотах <» = «)„ и «) = - «)„. Переход к спектральной плотности решетчатого процесса может быть сделан в соответствии с формулой" (3.74).

Следует заметить, однако, что полученные результаты имеют малое практическое значение. Входной сигнал