Ограничимся пока случаем, когда на выходе импульсного элемента импульсы отстоят друг от друга на одинаковые интервалы времени Г = const и отличаются друг от друга по амплитуде при одинаковой длительности 77" = const (рис. 2.6,6). Этот случай соответствует так называемой амплитудно-импульсной модуляции 1-го рода.

Если время замыкания ключа мало по сравнению с периодом чередования Т и пос7-оянными времени непрерывной части и если сигнал на входе ключа в течение времени, когда он замкнут, практически постоянен, то

ИвпрврыЁиая часть

У

Т= canst у=const

Рис. 2.6. Импульсная система.

последовательность конечных по продолжительности импульсов на выходе ключа можно заменить последовательностью дельта-функций. Величина каждой дельта-функции (точнее, интеграла от нее по времени) будет пропорциональной значению сигнала на входе ключа в момент его замыкания.

Поскольку ключ замыкается в определенные моменты времени (О, Т, 2Т, ЗТ и т. д.), то сигнал на входе необходимо рассматривать именно в эти моменты времени. Хотя на выходе непрерывной части сигнал и непрерывен, будем рассматривать его только в отдельные дискретные моменты времени.

Непрерывную часть совместно с ключом на ее входе будем называть импульсным фильтром (рис. 2.6, е). Более строго импульсный фильтр следует определить как устройство, которое получает входные сигналы и одновременно

дает выходные сигналы лишь в определенные моменты времени, например Т, 2Т, ЗТ и т. д. На входе непрерывной части с передаточной функцией W„{p) действует дискретная функ-Щ ция е*[пТ], где п = 0,

±1, ±2, ±3 и т. д.

В соответствии со сказанным эта функция может быть представлена в виде последовательности дельта-функций.

На выходе будет непрерывная функция, определяемая в эти же дискретные моменты времени: у (t) = y[nT], где п = 0, ±1, ±2 и т. д.

Решетчатые функции. Введем понятие решетчатой функции времени f[nT], или, в сокращенной записи.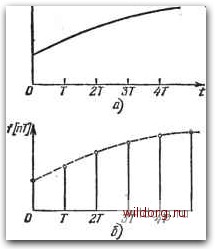

2Т ЗТ

• 4)

/[п], значения которой определены в дискретные моменты времени t = пТ, где п - целое число, а Г -период повторения. Операция замены непрерывной функции решетчатой

/М=/(01/-«г (2.17)

Рис. 2.7. Образование решетчатой показана на рис. 2.7.

функции. Изображенные на рис.

2.7, б ординаты представляют собой так называемые дискреты исходной непрерывной функции f(t) при t = nT (рис. 2.7, о). Дискреты f{t) могут быть также определены для смещенных моментов времени t = nT-\- AT = (n + е) Т. Смещение AT = const может быть положительной или отрицательной величиной при выполнении условия \AT\<iT. Относительное смещение е = АТ Т~ по модулю меньше единицы.

Образование смещенной решетчатой функции f[nT, AT], или, в сокращенной записи, f[n, е], из непрерывной функции f(t) для случая АТ>0 изображено на рис. 2.7, е.

В последующем изложении будем считать, что в решетчатой функции f[n, е] аргумент пО и параметр е>0. В случае необходимости рассмотрения функции f[n. Во] с отрицательным параметром ео<;0 дискретное время можно представить в виде [(п-1) + (1+ео)]7 = [(п-+ 7". Тогда решетчатая функция может быть записана в виде f[(n-l), е], где е=1+го-

Решетчатая функция не обязательно должна формироваться из некоторой исходной непрерывной. Любая числовая последовательность некоторой величины, определенная в дискретные равноотстоящие моменты времени, может быть представлена в виде решетчатой функции.

Обратная задача - формирование непрерывной функции из решетчатой - не может быть решена однозначно, так как функции, заданной в дискретные моменты времени, может соответствовать бесконечное множество непрерывных функций. Непрерывные функции, совпадающие с заданными дискретами, называются огибающими решетчатой функции.

Аналогом первой производной непрерывной функции для решетчатой функции является либо первая прямая разность

Af[n]=f[n+l]-f[n]. (2.18)

либо первая обратная разность

V/[«] = /[«]-/[«-!]. (2.19)

Обе эти разности показаны на рис. 2.8. Разности могут быть определены и для смещенных решетчатых функций f[n, е]. Однако формулы для ефО и е = 0 здесь и далее оказываются идентичными, вследствие чего в дальнейшем изложении принято е = 0.

Прямая разность определяется в момент времени t==nT по будущему значению решетчатой функции при t -=« = {п+\)Т. Это можно сделать в тех случаях, когда будущее значение известно. Обратная разность определяется для момента времени t = nT по прошлому значению решетчатой функции в момент времени (л ~ 1) Т,