Of -.AM{(f°)n 218)

Рис. 3.19. Петлевая нелинейная характеристика.

В случае однозначной нелинейности F (х) расчетная формула приобретает вид

дО = / \ Р (х + хО) {х) dx-P. (3.219)

°х " -оо

В более общем случае, когда F = F [х, рх), а также при наличии петлевых нелинейных характеристик формула (3.219) получается более сложной. Она может быть получена при использовании тех же обобщений, которые были сделаны при нахождении формул (3.216) и (3.217).

Для нелинейности более общего вида F=F{x, рх) формула получается в виде

оо оо

F= \ 5 F{X + x9, рХ + рх>){х, px)dxd(px). (3.216)

-оэ-со

Формула (3.216) может быть, в частности, использована для определения математического ожидания F в случае нелинейных петлеобразных характеристик. Так, для характеристики, изображенной на рис. 3.19, для случая симметричной функции распределения можно получить

F= ] F{% + x)b{x)dx +

\ 4 [Fx {% + х«) + Fa (X + ) ] о (х) d;c + F (X + х«) « {х) dx.

(3.217)

Эквивалентный коэффициент передачи для случайной составляющей можно определить следующими способами.

Первый способ предполагает использование среднеквадратичных отклонений O.V и Ор. Эквивалентный коэффициент передачи находится по их отношению

Второй способ предполагает определение эквивалентного коэффициента передачи из условия минимума математического ожидания квадрата разности истинного значения f и ее заменяющего значения (3.214). Это условие имеет вид

(3.220)

Из него можно получить

М {рохо}

= mm.

М {(0)2}

(3.221)

где Г/лс - значение взаимной корреляционной функции переменных F w х при т = 0. Если нелинейная зависимость носит однозначный характер, то из (3.221) имеем

со со

9" = 5 WO(A;)dx = J F{% + >fi)xPb{x)dx. (3.222)

* -со -CO

Эта формула также может быть обобщена на случай F = F{x, рх) и для петлевых характеристик по образцу формул (3.216) и (3.217).

Второй способ определения эквивалентного коэффициента передачи приво,п,ит к более простым формулам. С точки зрения точности расчета оба метода примерно равноценны. В некоторых случаях первый метод дает завышенные значения для оценки корреляционной функции величины/ (О, а второй - заниженные. Поэтому существует рекомендация [94] использовать для расчета среднее значение двух эквивалентных коэффициентов передачи, определенных двумя способами.

Кусочно-линейные характеристики. При расчете нелинейных систем часто используется замена нелинейной характеристики ее кусочно-линейной аппроксимацией. Пример такой характеристики изображен на рис. 3.20. Абсциссы bi и 2 соответствуют точкам излома характеристики, а коэффициенты Ci, ch и Cg представляют собой коэффициенты наклона соответствующих линейных отрезков.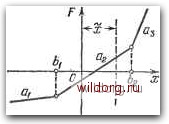

Рис. 3.20. Кусочно-линейная характеристика.

Применительно к такой характеристике формула (3.222) может быть представлена в следующем виде:

г ь, bj

</> = 1 аг(х)Ч (х) dx+a, (хГ О (х) dx+

+ las(xfff{x)dx

(3.223)

Каждый из входящих в (3.223) интегралов может быть выражен через дисперсию al и вероятность нахождения x(t) в рассматриваемом интервале. В результате вместо (3.223) можем записать

qO = aiPi (-oo<x<bi)+a2Pi(bi<x<:b2) +

+ Gs.Ps(62<a:<oo). (3.224)

Обобщая это на случай произвольного числа линейных участков, имеем

= 2 «Л.

i = l

(3.225)

Эта формула оказывается во многих случаях сравнительно простой, так как соответствующие вероятности Pj могут быть определены через интеграл вероятностей. Так, например, для характеристики, изображенной на рис. 3.20, имеем для нормального распределения

+ еф(Ьу (3.226)

Характеристики с разрывом непрерывностей. Встречаются характеристики, имеющие разрывы непрерывностей в виде скачков выходной величины. К таким характеристикам, в частности, относятся все релейные характеристики.

На рис. 3.21 изображен отдельно подобный скачок характеристики. Определим составляющую эквивалентного коэффициента передачи случайной величины х. Для этого воспользуемся формулой (3.222),