(вообще подвижных объектов) часто используется аппроксимация корреляционной функции в виде

K(T) = Doe-»*l-4cospT, (3.68)

где р - преобладающая частота, а р-коэффициент нерегулярности. При р = 0 процесс представляет собой так называемую регулярную качку, т. е. гармоническое движение с амплитудой А = )/2Do и случайной фазой.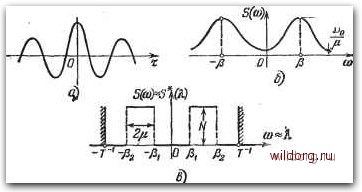

Рис. 3.9. Корреляционная функция и спектральные плотности сигнала типа нерегулярной качки.

Корреляционная функция (3.68) изображена на рис. 3.9, а. Она используется также для аппроксимации реальных корреляционных функций и иных случайных процессов, не связанных с качкой какого-либо подвижного объекта, в тех случаях, когда корреляционная функция носит затухающий колебательный характер. Спектральная плотность такого процесса

5(0))=- e-t*NicospTe--dT =

- СО

= pD(,

2(iDo (l +

cD„(l-fto2)

(3.69)

где a-

Р2+Ц2 p2 + j,2

9.. («.г-Ь i.«)-i. fc-(pM-pV-

Недостаток аппроксимации вида (3.68) заключается в том, что дисперсия первой производной рассматриваемой случайной величины Di-s-co. В этом нетрудно убедиться, умножив S (ю) на квадрат частоты и проинтегрировав полученную спектральную плотность в бесконечных пределах.

Для устранения этого недостатка используется другая форма аппроксимации в виде

К (г) = Doe-(-4 (cos рт+ 1 sin Р i т ). (3.70)

Этой корреляционной функции соответствует спектральная плотность (рис. 3.9, б)

5(0)).

2р+со

2aD„

ll+ajui+bUW Р*

(3.71)

где a2ii +у,\ +

Интегрирование спектральной плотности coS (со), которая соответствует производной рассматриваемой величины, в бесконечных пределах дает дисперсию производной

J CDS(C0)d(D =

- ео

Однако дисперсия второй производной рассматриваемой случайной величины стремится к бесконечности, что указывает на несовершенство и аппроксимации вида (3.70).

Для решетчатого случайного процесса типа нерегулярной качки корреляционная функция может быть получена из (3.68):

К [т] = Doe-II cos PmT. Ей соответствует спектральная плотность

(3.73)

5*(Я) =

(3.74)

1б8 СПУЧАЙНЬШ ПРОЦЕССЫ в ЦИФРОВЫХ СИСТЕМАХ [ГЛ. S

Обычно имеют место неравенства рГ1 и РТ"! и спектральная плотность может быть представлена в приближенном виде:

flD„(l-b62«)(l-b)

где a = 2p(p + pV. (P + pV- Формула (3.75) совпадает с (3.69) при замене ю = Я и умножении на

Для решетчатого случайного процесса типа нерегулярной качки более совершенная форма корреляционной функции может быть получена из (3.70):

К И = Doe-»*lI (cos рТт -f - sin рГ m ). (3.76)

Если рГ1 и рГ1, то спектральная плотность для псевдочастот Я <; практически совпадает со спектральной плотностью (3.71) при замене (1)==Я (рис. 3.9,6)

и умножении на Т-у-Л---)-

Удобная форма аппроксимации спектральной плотности 5(ю), для которой существуют ограниченные по величине производные случайной величины всех порядков, изображена на рис. 3.9, е. Если Р2<Т"\ то спектральная плотность 5* (Я) практически совпадает с S (ю), а псевдочастота Яяю.