448 синтез цАС при неизвестных Характеристиках [гя. в

Здесь Zi (р) и Za (р) - операторные сопротивления ветвей электрического контура.

В случае малого сопротивления источника (i?„«=«0) и большого входного сопротивления (R-yoo) формула (5.212) вырождается в передаточную функцию делителя напряжения

(Р) - Е(р) и, (р) - 2, (р) + Z, (р) • (5.213)

Передаточная функция (5.213), как правило, соответствует звеньям с лучшими корректирующими свойствами по сравнению с формулой (5.212).

Пассивные дифференцирующие звенья имеют свойства подавлять низкие частоты. Если восстановить на низких частотах прежний коэффициент усиления, что достигается введением дополнительного усиления йд = Оо, то передаточная функция дифференцирующего звена совместно с дополнительным усилителем равна

И„з(р) = {Тг>Т). (5.214)

Такое звено обладает свойством поднимать верхние частоты в TjTi раз. Пассивные интегрирующие звенья подавляют высокие частоты, а интегро-дифференцирую-щие звенья подавляют некоторый диапазон средних частот.

Фазосдвигакхцие звенья обладают свойством вносить отрицательный фазовый сдвиг при равенстве единице модуля частотной передаточной функции, Л((о) = 1. В связи с последним обстоятельством они иногда называются звеньями с бесконечной полосой пропускания.

Антивибраторы по своим свойствам противоположггы консервативным звеньям и на резонансной частоте имеют коэффициент передачи, равный нулю.

Параллельные корректирующие устройства используются обычно для введения в закон управления интегралов и производных. Для повышения порядка астатизма служат изодромные устройства (рис. 5.38, а), представляющие собой интегратор, включенный параллельно основному каналу. В качестве интегратора может быть использован интегрирующий привод [7] либо операционный усилитель в режиме интегрирования.

Передаточная функция изодромного устройства имеет вид

1ГЛр)=1 + п(р)=1+=1

(5.215)

где Ти =/гй- постоянная времени изодромного устройства. Логарифмические характеристики, соответствующие (5.215), изображены на

рис. 5.38, б. Как видно из этих характеристик, воздействие на амплитуду и фазу сигнала наблюдается только для частот to < Гй. Поэтому введение подобного звена в канал управления деформирует л. а. х. и л. ф. X. системы только в области низких частот. Это показано на рис. 5.38,е, где Lo(cu) и 1]9о((о) соответствуют асимптотической л. а. X. и л. ф. X. исходной системы. Штриховой линией показаны резуль-тирующиехарактеристики.

При соответствующем выборе величины постоянной времени результирующие л. а. X. ил. ф. X. в среднечастотной области (в районе пересечения л. а. X. оси нуля децибел)

могут практически не отличаться от исходных, что позволяет повысить порядок астатизма системы (ввести интеграл в закон регулирования) без заметного снижения запаса устойчивости.

Для введения в закон управления двух или более интегралов могут использоваться два и более изодромных устройства (рис. 5.39, а). В случае использования двух изодромных устройств их результирующая передаточная функция равна

1 . 1 \ (1-ЬГи1Р)(1 + ад 5216)

Рис. 5.38. Иводромное устройство и его характеристики.

TiTiP

Асимптотическая л. а. х. и л. ф. х. для систем точной функцией (5.216) изображены на рис Как и ранее, при выборе достаточно больших Тк1 и можно получить повышение порядка на две единицы без заметного снижения запаса вости системы регулирования.

Однако следует заметить, что постоянные изодромных устройств (как в случае включени

с переда-. 5.39, б.

значений астатизма устойчи-

времени я одного.

€>- Жр)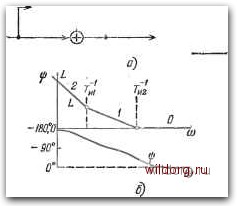

Рпс. 5.39. Двойное иводромное устройство и его характеристики.

так и в случае двух) не могут выбираться без учета положения запретной зоны для системы управления по точности (рис. 5.5).

Структурная схема введения производной в канал управления показана на рис. 5.40, а для идеального дифференцирующего звена и на рис. 5.40, б для реального звена с замедлением. На этих же рисунках показаны логарифмические амплитудные частотные характеристики приведенных схем.

Как уже отмечалось выше, обратные связи в линейных системах могут быть сделаны эквивалентными по своему действию последовательным и параллельным корректирующим средствам, что устанавливается формулами перехода (5.211). Однако отрицательные обратные связи имеют ряд преимуществ при работе в нелинейных