более общим выражением:

2N - 1

6i = M"* = 2 /i(6an])exp(-/-Jv). (6.Б7)

Это выражение можно упростить, если учесть, что fi=- + A при v = 0 и /i = -у -Aj при всех остальных значениях v. Тогда

2N - 1

2/V-1

(6.58)

так как сумма членов вида ехр[- ]-v) при v = 0, 1,...

2N-1 равна нулю. Из (6.58) получается нормированный коэффициент гармонической линеаризации

9* =

Расчет параметров периодического режима, когда Ле = - N - целое число, не представляет труда. По значению ошибки в установившемся режиме определяется относительный полупериод колебаний Л (6.56). Затем из (6.4) находится амплитуда колебаний на выходе системы:

(/ж) = 1*(Аа)1 (6.60)

где Я/v определяется формулой (6.44). На рис. 6.12 показано графическое построение для N = 2.

Если Ne представляет собой дробное число, то колебания носят квазипериодический характер. Их приближенный расчет может быть сделан следующими методами.

1) Введем предположение, что при переходе от одного периодического режима с целым значением N = No к другому с новым целым значением = Ло + 1 амплитуда первой гармоники и частота усредненного периодического режима изменяются непрерывно и плавно. Для частоты колебаний это полностью подтверждается формулой (6.54). Тогда для расчега амплитуды первой гармоники колеба-

НИИ МОЖНО воспользоваться тем же графическим построением (рис. 6.12) и формулами (6.54) и (6.60) при замене в последней на iVj. и а на mo = nN-.

2) Второй метод заключается в том, что для усредненного периода колебаний, изображенного на рис. 6.13, а с учетом действия экстраполятора (пунктирная линия), находится обычными приемами разложения в ряд Фурье амплитуда первой гармоники:

Далее может быть определена амплитуда колебаний на выходе системы пересчетом Ci на вход (умножением на 6i) и умножением на модуль частотной передаточной функции разомкнутой системы:

ai = 6ici U7(e/»") = 261

2/Vc

W* (Ao) 1. (6.62)

Здесь

cuo =

2/Vc

(6.63)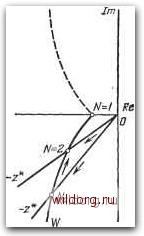

Рис. 6.12. К расчету периодических и квааипе-риодических режимов.

- круговая частота и псевдочастота периодического режима (частота преобладающей гармоники).

3) Возможно использование способа расчета, когда рассматривается некоторый дополнительный усредненный режим движения tft) на выходе непрерывной части (6.13, б), полученный припасовыванием на интервалах времени О-ьТи T-i-To = 2NT. Далее в случае необходимости можно выделить в этом режиме первую гармонику. В отличие от предыдущих двух методов, здесь расчет может производиться и в тех случаях, когда время существования на выходе экстраполятора сигнала (m+l) б не подчиняется условию Л=1, а может содержать произвольное число тактов.

Пример 6.1. Пусть передаточная функция непрерывной части

W7„(P) =

(6.64)

Дискретная частотная передаточная функция разомкнутой системы

(6.65)

где /Ci = АнАц - общий коэффициент усиления разомкнутой цепи с присоединенным коэффициентом передачи ЦВМ.

W* (/Я) = D* (/Я) Wt (/Я) = 1 Го* (УЯ) =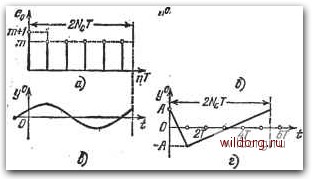

Рис. 6.18. Зависимость среднего полупериода от установившейся ошибки.

Режим симметричных колебаний при e = 0,56i построен на рис. 6.13,6. Амплитуда может бьць найдена методом припасовывания:

А = Ц1. (6.66)

Так как из условий устойчивости KiT<.2,то i4<0,56i. Относительный полупериод Л= 1. Первая гармоника этого колебательного режима имеет амплитуду

8 fi, К{[ 2fiiKtr

«2 2

(6.67)