При интегрировании этой спектральной плотности в соответствии с формулой (3.44) получается дисперсия я/г

Нормированная спектральная плотность имеет здесь

0(ю) =

(3.58)

Спектральная плотность (3.56) изображена на рис. 3.7, а.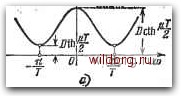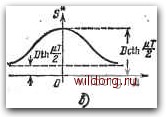

Рис. 3.7. Спектральные плотности сигнала с экспоненциальной корреляционной функцией.

Найдем теперь спектральную плотность рассматриваемого процесса в функции псевдочастоты. Используя формулу (3.48), получаем

2ГзО f 1 + 5*(Я) =----

(3.59)

Т (1 •

где эквивалентная постоянная времени

l+dT Т i.T » - l-d 2 "~ 2 2 •

Заметим, что при спектральная плотность S* (Я)

переходит с точностью до множителя Т в спектральную плотность непрерывного случайного процесса, соответствующего корреляционной функции К (т) = Dexp (- л т ):

2ГвО

Пт TS* (Я)=Ит---

(3.60)

Интегрирование выражения (3.59) в бесконечных пределах в соответствии с (З.бО) также дает дисперсию

1 in

D. (3.61)

График спектральной плотности S* (Я) близок по своему виду к графику спектральной плотности соответствующего непрерывного процесса (3.60). Он построен на рис. 3.7,6.

Процесс с равномерным спектром в ограниченной полосе частот, В непрерывных системах часто используется

Рис. 3.8. Равномерная спектральная плотность в ограниченной полосе частот.

аппроксимация спектральной плотности случайного процесса белым шумом с ограниченной полосой (рис. 3.8, а). Этой спектральной плотности соответствует корреляционная функция

COS сот dco =

Ы sin (j,T Dp sin р.т

JtT ~ ЦТ

(3.62)

Корреляционная функция построена на рис. 3.8, б.

Достоинство подобного представления характеристик случайного процесса заключается в том, что оказываются ограниченными дисперсии производных всех порядков. Действительно, для производной -го порядка дисперсия может быть определена [8] по формуле

(3.63)

Формула (3.63), в частности, может быть использована для определения диапазона частот ± р. Если заданы зна-

- I .urd-coscoTcosiT) J• (3.66)

Однако использование ее затруднено сложностью полученного выражения (3.66).

Рассмотрим спектральную плотность S* (К) вида, изображенного на рис. 3.8, в. Если [л,<Т-, то на основании приближенной формулы (3.51) получаем

(3.67)

sin цтГ Dp sin цтГ "~ тпТ ~ \лтТ

Последнее выражение полностью соответствует корреляционной функции (3.65). Так как для частот ю<Г-1 псевдочастота Я = 27 tg 0,5(йГ ю, то пределы изменения частоты ± [г на рис. 3.8, а и рис. 3.8, в практически совпадают.

Нерегулярная качка. Для описания случайных непрерывных процессов типа нерегулярной качки морских судов

чения дисперсий случайного сигнала Do и его первой производной Dl, то из (3.63). следует:

(3.64)

Рассмотрим теперь случай, когда этот случайный процесс представляет собой производящую функцию для решетчатого случайного процесса. Здесь можно выделить два случая.

Если спектр относительно широк и выполняется условие 1)1,>Т~, то такой процесс сводится к дискретному белому шуму.

Если спектр относительно узок и выполняется условие [l<T-, ТО корреляционная функция решетчатого процесса будет

Спектральная плотность 5(6/"), соответствующая (3.65), будет определяться выражением