fXniax =arctgp + Дф,

(5.262)

Далее можно воспользоваться методикой, изложенной в § 5.3. Тогда для получения заданного запаса устойчивости, определяемого по величине показателя колебательности, необходимо выполнить условия

функцией UJa (р) = 1, а фазовый канал - звено с передаточной функцией

«?ф(р) = [ (Т1>т.). (5.258)

В этом случае амплитудная характеристика разомкнутой системы в соответствии с выражением (5.257) будет

IW (7(0)1 , -. (5.259)

i= 1

Фазовая характеристика Ф (со) = Ф„ ((0) + Фпу ((О) = - 180° +

+ arctg coTi - arctg сота - 2 arctg соГ, + Лф, (5.260)

где дополнительный фазовый сдвиг

Аф = - 24° sin 2фф = - 24° sin 2 (arctg coti - arctg соТа). Приближенное выражение для запаса по фазе: [X = 180° + ф (со) arctg coTi - arctg со (т + Ts), (5.261) <?

где = 2 Ti. Исследование запаса по фазе на максимум 1=1

дает

где базовая частота соо = УК2, а величина h определяется из выражения

arctg

- Дф

(5.264)

В таблице 5.9 приведены требуемые величины h при различных значениях показателя колебательности М.

Таблица 5.9

Для типовой л. а. х., изображенной на рис. 5.46, б, непрерывная часть системы описывается передаточной функцией

WAp)---. (5.265)

рП il + TiP)

Расчет здесь можно вести аналогично, если использовать вместо базовой частоты (йо = УК2 (рис. 5.46, а) базовую

частоту cuo = y/CiTr.

Условия применимости полученных результатов в цифровых системах остаются подобными тем, которые были изложены в начале настоящего параграфа. Если период дискретности Т выбран достаточно малым так, что в районе малых и средних частот выполнялось бы условие Х}(й, то все расчеты сохраняют свою силу.

Реализация псевдолинейного корректирующего устройства производится следующим образом. Дискретная частотная передаточная функция фазового канала в соответствии с таблицей 5.8 имеет здесь вид

117* /п\ 1-" H-Ai "Ф (A)-i fc i+yu,

(5.266)

Ей соответствует дискретная передаточная функция

z-a 1-аг-» 5267)

477 / S < -" 1 - az

и7ф() = Г=б = Г1бГ7-

Структурная схема рассматриваемого псевдолинейного устройства в дискретном варианте изображена на рис. 5.47.

Псевдолинейные корректирующие устройства имеют крупный недостаток, который ограничивает их использование в системах автоматического управления. Он заключается в том, что все приведенные выше характеристики и расчеты справедливы лишь для случая, когда постоянная составляющего сигнала на входе равна нулю. Появление даже сравнительно небольшой постоянной составляющей может вызвать резкое ухудшение всех характеристик и потерю устойчивости системы. Это приводит к тому, что использовать эти устройства можно лишь в тех случаях, когда система обладает астатизмом по отношению к возможным воздействиям на нее или когда этот астатизм специально обеспечивается введением в систему изодромных устройств.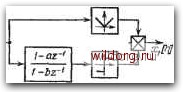

Рис. 5.47. Дпскретное псевдолинейное звено с положительным фазовым сдвигом.

C(z)

а т

Biz)

§ 5.6. Комбинированное управление

Использование комбинированного управления позволяет снизить требования к основному каналу и получить лучшие

качественные показатели системы управления. Комбинированное управление особенно удобно применять в тех случаях, когда задающее воздействие вычисляется на ЦВМ. Тогда вычисление производных задающего воздействия оказывается наиболее простым. Подобное положение может быть, например, при слежении за любыми объектами по счислимым координатам.

Структурная схема цифровой системы комбинированного регулирования изображена на рис. 5.48. Дополни-

Рис.

5.48. Система комбинированного управления.