мулу (3.4) для независимых случайных величин, получим

оо оэ

/?[сю]= 5 Xi&{Xi)dXi- 5 а:2* (лгг) йлгг = (JJ) = (х)

- оо -оэ

4. Значение корреляционной функции при т = 0 является ее наибольшим значением (рис. 3.4). Докажем это. Рассмотрим очевидное неравенство

(х[п]-х[п + т\)0.

Сделаем преобразование

[п] + х" [п + т] 2х [п] л: [п + т].

Возьмем среднее по времени от правой и левой частей. В результате получим

xn] + x[n + m] = 2x = 2R[0],

2х[п]х[п + т] = 2R [т].

Отсюда вытекает доказываемое неравенство: R [0]:R [щ].

5. Значение корреляционной функции чаще всего будет тем меньше, чем больше промежуток времени т = тТ,

-10 -8 ?

4 6 i, i -4 -ZD

Рис. 3.4. Пример корреляционной функции решетчатого случайного стационарного процесса.

так как связь между далеко отстоящими друг от друга значениями х будет обычно слабее. Увеличение временного сдвига т может происходить при увеличении числа т и при увеличении периода дискретности Т.

6. Чем менее инерционен (более подвижен) объект наблюдения и чем больше период дискретности Т, тем быстрее убывают R\m\ и К\т\ с увеличением числа т. Отсюда следует, что, чем быстрее убывает корреляцией-

ная функция, тем болыние частоты будут присутствовать В случайном процессе.

Таким образом, при известной корреляционной функции легко определяются следующие вероятностные характеристики:

а) среднее значение (момент первого порядка)

x = x = VR М;

б) средний квадрат (начальный момент второго порядка)

x2 = x2 = i?[0];

в) дисперсия (центральный момент второго порядка)

D = R[0]-R[oo] = Km

г) среднеквадратичное отклонение

o=Vo=VR[0]-R[<=VT\o].

Корреляционную функцию можно найти на основании экспериментально снятой кривой случайного процесса

при наличии достаточно длительной записи (рис. 3.5). Обработка имеющейся осцилограм-мы производится следующим образом. Весь интервал записи осциллограммы Tq делится на Л равных частей, длительность которых равна периоду дискретности Т. Затем для различных значений г = тТ находятся средние значения произведений ординат

И] = 7 2 (3.28)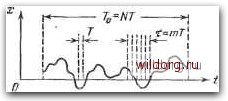

Рис. .я.."). Обработка осцилограммы реализации случайного процесса.

По ЭТИМ значениям строится график корреляционной функции в зависимости от интервала т. Этот график может быть аппроксимирован затем некоторой функциональной зависимостью.

Корреляционную функцию можно найти по результатам эксперимента также при использовании специальных

= 1т5л7ПП у. isin(a3inr-fiji)sin(a3inr-t-a3imr+iji)=

= jim2j 2 f [cosa3inr-cos(2cDinr-t-a3imr-t-2%)],

n = -N

При выполнении условия 2а)1Тф2кл {k=l, 2, ...)

Тогда имеем

R [т]= 2 cobCDimr.

приборов -корреляторов, которые автоматически вычисляют среднее произведение двух ординат осциллограммы, отстоящих друг от друга на расстояние х = тТ.

Если найденная корреляционная функция R [т] содержит постоянную составляющую x = \/R[co], то, выделив ее, можно перейти к корреляционной функции /С[т] в соответствии с (3.20), т. е. К[т] = R[m\ -(х).

Можно также ввести в рассмотрение нормированную корреляционную функцию

PI"]- D /? [0]-/?[со] • -

которая удобна тем, что всегда р[0]=1.

Корреляционная функция К[т\ для неслучайных (регулярных) функций времени тождественно равна нулю. Однако корреляционная функция R [т] может вычисляться и для неслучайных функций времени. Рассмотрим несколько примеров.

1. Для постоянной величины х[п] = Ло (например, для постоянного тока) корреляционная функция

n=-N

2. Для гармонической функции х[п] = Aisin((i)inT-]-<i) корреляционная функция

R[m]==