Центрированное значение этой передаточной функции совпадает с тем, что дает формула (6.106), т. е. W%(z) = = Wn (2). Это определяется исключением всех полюсов z=l из изображения выходного сигнала.

Установившуюся периодическую реакцию линейного дискретного фильтра на произвольный симметричный периодический сигнал можно найти по матричному равенству y = we, где y = \\yi\ и е= ЦеЦ-матрицы-столбцы входных и выходных величин размером Nxl, & прямоугольная матрица коэффициентов размером NxN

В частном случае симметричной прямоугольной волны на входе, когда е = ео, е, .... ef, дискреты периодического режима на выходе будут равнь! сумме коэффициентов соответствующей строчки (6.107), умноженной на величину во-

Условия замыкания. Для того чтобы периодический режим рассматриваемого вида мог бы существовать, необходимо выполнение условия замыкания. Оно сводится здесь к тому, чтобы движение на выходе системы, т. е. у (t), вызывало бы появление на входе канала закона изменения сигнала ошибки е [п] рассматриваемого вида.

Это поясняет рис. 6.18. Он соответствует рассмотрению двух видов периодических режимов относительно точки 2 (рис. 6.7, а). Рис. 6.18, а соответствует случаю существования на входе простейшего симметричного периодического режима в пределах единицы младшего разряда (рис. 6.8). Пусть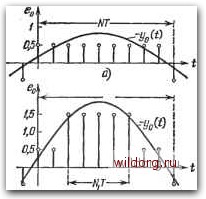

Рис. 6.18. Примеры конфигураций периодических режимов.

амплитуда непрерывного гармонического входного сигнала Уо (О = Г У (О лежит в пределах О < Л67 < 1, где 61 - цена единицы младшего разряда входного преобразователя. Тогда последовательность дискрет на его выходе ео[п] будет иметь вид прямоугольной волны (рис. 6.18, а), высота которой равна 0,5. При этом фазовый сдвиг для непрерывного входного сигнала должен лежать в пределах 0<;(р<;лЛ-1. Эти условия являются достаточными для того, чтобы на выходе преобразователя существовал бы сигнал принятой конфигурации.

Указанное условие для фазового сдвига входного сигнала эквивалентно наложению условия на фазовый сдвиг выходного сигнала канала в виде О < л-j-я); < лЛ",, которое сводится к условию для запаса по фазе [лл--я/ в виде (Xix<nN-.

Более строго, сигнал указанной конфигурации будет существовать при выполнении достаточного и необходимого условия

1>ео[г]=- Уо [г] = sin (I г + (р)> О, (6.108) где /• = 0,1, ..., N-\, и, соответственно,

- К ео И = sin( / -f ф) < О, (6.109)

где l = N, N-\-l, 2N-1. Заметим, что случаи ф = 0 (или (л = 0) и Ц) = nN- (или (л = лЛ-) относятся к неопределенным и требуют дальнейшего исследования с учетом дополнительных факторов: малых параметров, гистере-зисной петли в характеристике преобразователя Н-К и др.

Если в результате прохождения этого сигнала через канал управления на выходе будет существовать изменение управляемой величины уо (/), показанное на рис. 6.18, а сплошной линией, то условие замыкания выполняется и подобный режим существовать может.

Непрерывный сигнал на выходе системы может и не быть гармоническим. Однако необходимо сохранение главного условия, чтобы этот сигнал после прохождения через нелинейный элемент (входной преобразователь) генерировал сигнал той же формы, которая была принята во входном сигнале канала управления. В этом и заключается условие замыкания и условие возможности длительного существования периодического режима данной формы.

венства:

2>-(S+*)>. >"(#++p)>»

(6.110)

Для каждых конкретных значений Л и ф могут быть определены возможные значения N и Ni, и, наоборот, по заданным значениям N и Ni можно определить пределы возможных значений Л и ф. Для этой конфигурации сигнала также могут быть сформулированы достаточные и необходимые условия применительно к дискретным значениям ео[п], аналогичные (6.108) и (6.109).

При исследовании возможных несимметричных режимов следует учесть, что начало отсчета в нелинейной характеристике входного преобразователя (рис. 6.7, а).

Однако следует обратить внимание на то обстоятельство, что в пределах некоторой возможной зоны отклонения L/oit) от кривой, изображенной на рис. 6.18, а, режим на выходе преобразователя, в соответствии с рис. 6.7, б, изменяться не будет. Это означает, что система оказывается фактически разомкнутой в пределах возможной зоны изменения процесса </о(/), не нарушающего характера изменения выходного сигнала преобразователя.

Поэтому вопрос устойчивости возможного периодического режима должен рассматриваться применительно к разомкнутому каналу управления. Если этот канал устойчив, что требует устойчивости объекта управления, то возможный периодический режим будет также устойчив. Если объект управления нейтрально-устойчив или неустойчив, то рассматриваемый возможный режим не может существовать длительно вследствие наличия медленных уводящих движений. Поэтому возможные периодические режимы оказываются неустойчивыми и в системе будет существовать сложный квазипериодический режим с непрерывным переходом от одного возможного вида простейшего режима к другому.

Изображенный на рис. 6.18, б симметричный периодический режим соответствует более сложному случаю, когда для амплитуды гармонических колебаний должно выполняться условие 6i < Л < 26i. Кроме условия О < <Ф<лЛ/- здесь должны выполняться еще два нера-