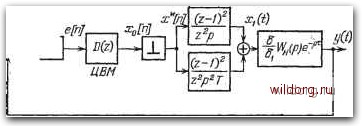Рис. 2.18. Упрощенная структурная схема ЦАС с экстраполятором первого порядка.

т = 0, период повторения Г = 0,1 с, цена младшего разряда входного преобразователя 6i = 0,l град, цена младшего разряда выходного преобразователя 6 = 0,05 В.

Для экстраполятора нулевого порядка в соответствии с формулой (2.136) имеем

-1 кТг

W7„(2) = £:l*-i;U

Si 2 (2-1)2

6 k„T КпТ

~S,2-1 г-\~г-\

где /<н = б7 6А:„ = 50 с-.

Для экстраполятора первого порядка в соответствии с формулой (2.143) имеем

- А flu. Г AZ!?

k,Tz<z+l)

2(2-1)3

/<:.,Г(Зг-1) - 22(2-1)

2,5 (3z-I)

2(2-1)

Последнее выражение позволяет изобразить структурную схему одноканальной ЦАС так, как это показано на рис. 2.18.

При мер 2.2. Определим передаточную функцию непрерывной части, если объект имеет передаточную функцию

для случаев, когда используется экстраполятор нулевого порядка и экстраполятор первого порядка. Примем следующие значения: „=100 град/В-с, запаздывание

Экстраполяторы более высоких порядков. Рассмотрим теперь использование экстраполяторов второго и более высоких порядков. Идея работы экстраполяторов заключается в использовании обратных разностей первого и более высоких порядков аналогично тому, как это было сделано в формуле (2.141). Вначале обратимся к экстра-полятору второго порядка.

На рис. 2.19 изображены штриховой линией изменения производящей функции x{t), в качестве которой для

/X(t)

О Cn-min-3-)nn-2)Un-f)T (тГ)Т t

Рис. 2.19. Экстраполирование выходной функции.

случая D (г) = 1 можно принять, как и ранее, величину b-be{t), и сплошной линией--требуемый закон экстраполирования Xi{i) на участке пТt<z.{n-\-\)T. На участке экстраполяции изменение выходной величины должно соответствовать квадратичной параболе

t-tiT . (t-tiT)

Xi(t - nT) = x[n] + ai

(2.144)

Запишем условия прохождения этой парабо.лы через точки, соответствующие времени t - nT = - Т и t - nT = = - 2Т:

х[п-Ц = х[п\-аг + , х[п-2\ = х [ti\ - 2gi + 2щ,. Отсюда можно найти ai = 0,5(3x[rt]-4xf«-l] + x [n-2]) = s! х[п\ +

а2 = х[п\ - 2х{п- 1] + л;[п -2] = v-«W-

Следовательно, формула экстраполяции (2.144) приобретет вид

x,(t-nT)4n] + (yx[n] +

+ Vx[n]ff. (2.145) Вводя новую переменную u = {t - пТ) Т~, имеем Хг {Ти) = х[п] + (ух [п] + и + ух[п\. (2.146)

Выражения (2.145) и (2.146) справедливы при пТ < t<{n-\-\)T или, соответственно, при 0ы<;1.

Аналогично проделанному выше можно показать, что в этом случае передаточная функция непрерывной части должна определяться по формуле

о() - i {"Р {( р + I + (Р) -(2-147)

При рассмотрении экстраполяторов более высокого порядка целесообразно использовать вторую интерполяционную формулу Ньютона [30], которая для рассматриваемого случая экстраполяции на участке пГ < <.(п+1)Т может быть записана в виде

х,{Ти)х[п] + /х[п]и + !угх[п]+...

»(»+1)(«+2)...(»+/-1), (2.148)

где u = {t - пТ) Т , а I - порядок экстраполятора. Так, например, если 1 = 2, то из (2.148) получается

Хг (Ти) = д; [«] + (V д: [л] + -) u + s/х [п] ,

что совпадает с формулой (2.146).

При/ = 3 формула" экстраполяции (2.148) будет иметь

X, (Ти) х[п] + (ух [п] + + ) и +

+ (VX [п] + s/x [«]) f + V [п] f. (2.149)