Для случая N=2 аналогичным образом можно получить

(6.39)

Амплитудно-фазовые характеристики представляют собой прямые линии, расположенные в секторе -180° ±45° (рис, 6.9,6).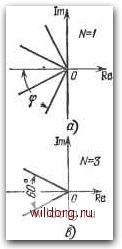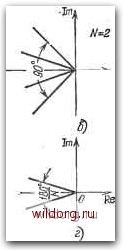

N>3

Рис. 6.9. Амплитудпо-фазовые характеристики нелинейного элемента.

При iV = 3 модуль IZ* I == I,5ai6/. Характериститш расположены в секторе -180° ±30° (рис. 6.9, в). Для Л>3

(6.40)

причем характеристики расположены в секторе -180"± ±Л"1-90° (рис. 6.9, г). При N->-oo, что соответствует непрерывному случаю, сектор расположения а.-ф. х. стягивается в линию, совпадающую с отрицательной вещественной полуосью.

Уравнение периодического режима имеет вид (6.4). Его можно решить графически (рис. 6.3) или аналитически. В результате, как это показано на рис. 6.10, с, для Л==1 амплитуда ошибки или, что все равно, амплитуда управляемой величины объекта

ci = 11Г (е/-) I =11( 1) I =1117* (/ОС) 1. (6.41)

Под знаком модуля в (6.41) находится значение частотной передаточной функции при (о=л/Т или при

1-уоо.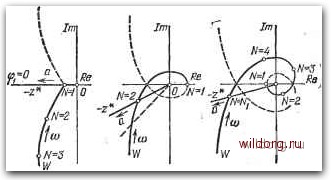

ф В) ф

Рис. 6.10. Графический расчет периодических режимов.

При колебаниях с относительным полупериодом TV = 2, если имеется точка пересечения двух годографов, как, например, показано на рис. 6.10,6,

«1

1. 2\

(6.42)

Аналогичным образом для колебаний при N 1 (рис. 6.10, в)

= r*(/V)l.

(6.43) (6.44)

Следует заметить, что в системе обычно могут существовать симметричные периодические режимы с различными значениями полупериода Л. При этом для каждого конкретного значения периодический режим в случае управляемого объекта без самовыравнивания (астатического) оказывается нейтрально-устойчивым относительно среднего значения управляемой величины. В результате этого ни один из симметричных периодических режимов с фиксированным значением не может существовать длительное время. Медленные движения объекта, вызванные наличием возмущений, приводят к непрерывным переходам периодических режимов от одного значения N = Ni к другому NNjNi.

Из всех возможных периодических режимов обычно наиболее тяжелым для системы с точки зрения влияния ограниченной линейности канала является режим при N=Nmm- Это связано с тем, что при использовании дискретных корректирующих программ ЦВМ, т. е. при D (2)71, более вероятно применение алгоритмов, эквивалентных дифференцирующим контурам, которые вызывают подъем высоких частот.

Выходная величина ЦВМ в режиме симметричных периодических колебаний может бьп-ь получена, если входную решетчатую функцию (рис. 6.8) пропустить через фильтр с передаточной функцией D{z). Это делается на основании формул § 2.7, которые позволяют вычислить параметры периодического режима на выходе дискретного фильтра при известных параметрах периодического режима на входе.

Покажем, как это делается для случая = 1, когда число гармоник оказывается равным единице. В соответствии с (2.204) амплитуда сигнала на выходе ЦВМ (рис. 6.1)

ЛГо шах - е„ шах I £» (б") 1 = е„ „ах 1 £» (- 1) j, (6.45)

где во и лго -цифровые представления входного и выходного сигналов ЦВМ. Пусть, например, в ЦВМ используется алгоритм (таблица 5.9)