Входной сигнал u{t) представляет многомерный случайный процесс типа белого шума с математическим ожиданием всех компонент, равным нулю.

В начальный момент времени t = to матрица-столбец x(to) характеризует начальное состояние системы и соответствует многомерной случайной величине с нормальным распределением. Это означает, что величины x(t) и go (О соответствуют многомерным нормальным процессам.

Матричная структурная схема, соответствующая уравнениям (4.124), изображена на рис. 4.13. Эта схема

u(t)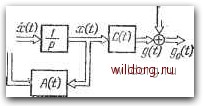

Рис. 4 ]3. Матричная структурная схема непрерывного формирующего ф1т.яьтра.

В части, соответствующей первому уравнению (4.124), и является формирующим фильтром для входного процесса системы управления. Схема содержит п интеграторов. Звено А (t) показывает связи в системе. Эта матрица имеет вид

«11(0 012 (t) ain(t)

(4.125)

А (t) = I "22 (О ... ап (О

aniiO an2(i) ...

Коэффициент Су (О есть коэффициент передачи по обратной связи с выхода /-го интегратора на вход i-ro интегратора. Подобным же образом могут быть записаны матрицы В и С.

В соответствии с теорией линейных дифференциальных уравнений все их решения могут быть выражены через фундаментальную матрицу Ф(/, to), являющуюся Переходной матрицей для системы уравнений. Эта матрица оказывается невырожденной, и она удовлетворяет дифференциальному уравнению

£51. = Л(/)ф,/, /о)

(4.126)

С начальными условиями Ф (О) о) = Л где / -единичная матрица размером пхп.

В стационарных системах л (О = const и ф(/, о) = = Ф(то), где XQ=t - to. Тогда уравнение (4.126) легко решается переходом к изображениям Лапласа

рФЛр)-/==лфлр),

откуда изображение фундаментальной матрицы

Далее можно перейти к оригиналу

ф(То) = <5?-М[р/-л]-П.

Для рассмотренного выше примера 4.3 матрицы коэффициентов имели вид

Обратная матрица

[р/-Л]-1:

Ьр + ар+\

Переход к оригиналам дает здесь

Ф{Хо)е-.-°Х

cos Рто + -р- sin Рто

-р sin рто

- Р (1 + sin К cos Рто-sin Рто I

где }х = 0,5с/Ь, а Р = 1/Ь" -Этот результат совпадает с тем, что было получено в примере 4.3.

В соответствии с (4.124) можно записать уравнение движения свободной системы-аналога:

=Л(<)(0.

Тогда решение для x{t)

х(/) = Ф(/, Qx{to).

(4.127) (4.128)

Таким образом, матрица Ф(/, о) соответствует линейному преобразованию, которое отображает состояние

g 4.Б] ОСНОВЫ таОРИИ ФИЛЬТРОВ КАЛМАНА 309

системы x(to) в состояние x{t). Поэтому она носит название переходной матрицы. Для переходной матрицы имеет место следующая зависимость:

Ф(2, /«) = Ф(4, /1)Ф(/1. /о). (4.129)

из которой вытекает равенство

Ф 41. о) = Ф(/о. /i). (4.130)

Для первого уравнения (4.124) можно записать решение через переходную матрицу:

л;(0 = Ф( to)xito) + \0(t, х) В (х) и (X) dx. (4.131)

Однако подобная запись решения имеет скорее методическое, чем практическое значение ввиду больших трудностей, связанных с использованием формулы (4.131).

Входной сигнал системы-аналога представляет собой многомерный случайный гауссов процесс с нулевым математическим ожиданием и корреляционной (ковариационной) матрицей

cov[«(0; u{t + x)] = M[u(t)u(t + x)] = Q(t)8(x). (4.132)

Здесь Q (t) - симметричная положительно-определенная матрица размером гхг, а б (т) - единичная дельта-функция. Начальное состояние системы-аналога характеризуется матрицей-столбцом x(t(,), который определяет многомерную случайную величину с гауссовым распределением, имеющую заданное математическое ожидание М[х(4)]=А-о и корреляционную матрицу

P(/o) = cov[x(g, xito)] = M{[xito)-Xo][x{to)-Xo]}. (4.133)

Здесь Р (/о) -симметричная матрица размером пхп. Она может быть, в частности, диагональной, элементы которой суть дисперсии компонент матрицы-столбца переменных состояния.

Измерительное устройство, которое используется для получения информации о наблюдаемых величинах системы-аналога, т. е. компонентах матрицы-столбца C{t)x{t), содержит всегда источник помех (ошибок измерения). Поэтому наблюдаемый сигнал записывается в виде

gAt)C{t)x{t) + v{t), (4.134)