§ 5.3. Общие принципы построения систем управления с заданным запасом устойчивости

Выполнение требований по точности должно сопровождаться обеспечением в системе управления необходимых запасов устойчивости. Проверка достаточности удаления системы от колебательной границы устойчивости может производиться различными критериями. Используются, например, такие оценки, как колебательность (отношение мнимой части корня характеристического уравнения к вещественной), запасы устойчивости по амплитуде и по фазе, перерегулирование, показатель колебательности и др. Все эти критерии, в общем, приводят к цели.

При использовании для расчета систем частотных методов и, в частности, логарифмических частотных характеристик удобно использование и частотных оценок запаса устойчивости. Для этой цели наиболее удобен показатель колебательности, равный отношению максимального пика амплитудной частотной характеристики замкнутой системы к ее начальной ординате при № = 0 (см. (2.200)).

На основании большого числа опытных данных рекомендуемый показатель колебательности лежит в пределах М = 1,3 1,7. В некоторых случаях, когда система регулирования должна быть очень хорошо задемпфирована, принимают М = 1,1 -5- 1,3 и даже М = 1. Значения показателя колебательности выше 1,7-ь 1,8 приводят к резкому возрастанию склонности системы к колебаниям. Слишком низкие его значения могут привести к серьезным трудностям при проектировании корректирующих средств.

Необходимым и достаточным условием того, чтобы в устойчивой системе показатель колебательности был не больше заданного, является нахождение амплитудно-фазовой характеристики (а.-ф. х.) разомкнутой системы вне запретной области (рис. 2.27, д и рис. 5.10), представляющей собой окружность [8]. Радиус этой окружности равен

= -М23Г (5-99)

а смещение центра влево относительно начала координат

С=л£г. (5.100)

Для оценки запаса устойчивости замкнутой системы по этой методике в непрерывном случае должна исполь-

СИНТЕЗ ЦЛС ПРИ НЕИЗВЕСТНЫХ ХЛРЛКТЕРИСТИКЛХ [ГЛ. 5

зоваться частотная передаточная функция разомкнутой системы W (/со). В цифровых системах можно использовать как передаточную функцию W (е*), так и передаточную функцию W* ЦК). Для удобства расчета по логарифмическим характеристикам целесообразно ориентироваться на передаточную функцию W* (/Я).

Дальнейшее изложение вопроса в настоящем параграфе касается общих положений по построению систем с заданным запасом устойчивости, как непрерывных, так и цифровых. Поэтому все требования.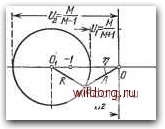

V=JmW(Jai)

UFeWffw)

которые будут сформулированы для частотной передаточной функции непрерывной системы IF (/со) и ее логарифмических характеристик, в равной степени относятся к частотной передаточной функции разомкнутой цифровой системы W* (/Я) и ее логарифмическим характеристикам.

Можно найти условие того, чтобы а.-ф. X. разомкнутой системы не заходила в запретную область. Это имеет место в том случае, когда запас по фазе а.-ф. х., определяемый выражением p=180°-fal5 (где фазовый сдвиг = arg W (/сй) для модулей Л = W (/со) , лежащих в пределах UxAUi (см. рис. 5.10)), не меньше требуемого запаса по фазе

Рис. 5.10. Запретная область для а. ф. X. разомкнутой системы.

Г) = arccos

= arccos

А+С 2АС

(5.101)

Здесь С определяется формулой (5.100). Максимальное значение запаса по фазе, которое требуется в районе точки В на окружности, будет в том случае, когда отрезок ОВ является касательной к окружности. Тогда А - = УС~Я = УС и, следовательно,

Timax = arccos = arccos -

- arctg

= arcsin

(5.102)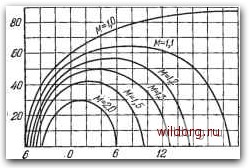

18 20ЦА,аБ

Рис. 5. II. Зависимость требуемого запаса по фазе от модуля в дебицелах.

зование кривых ri = f(201g) может заключаться в том, что для построенной л. а. х. разомкнутой системы по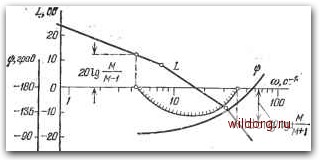

Рис. 5.12. Запретзая область для логарифмической фазовой характеристики.

точкам находится и строится требуемый запас по фазе (рис. 5.12), который откладывается от оси нуля децибел вниз. Построение ведется в пределах изменения модуля

20 Ig 20 Ig Л < 20 Ig (5.103)

По выражению (5.101) можно определить требуемый запас по фазе в функции модуля, выраженного в децибелах, для различных значений показателя колебательности М. Эти зависимости построены на рис. 5.11. Исполь-