412 синтез цас при неизвестных характеристиках гл. 5

является переходной функцией. На основании известных методов построения переходных процессов можно из (5.174) найти переходную функцию в нормированном виде, т. е. для относительного времени:

УЩ = go 11 + Ae- + {В sin р/о + С cos Щ е-»» ]. (5.175)

Подставляя в (5.174) значения относительных постоянных времени, соответствующих различным показателям колебательности, можно на основании (5.175) построить ряд переходных функций.

Таблица 5.1

Значения коэффициентов

В таблице 5.1 приведены значения коэффициентов (5.175) для различных показателей колебательности. По данным таблицы 5.1 построены кривые переходных процессов (рис. 5.27). Переходные процессы построены в нормированном виде: по оси ординат отложена величина ho{to)=goy{(i>ot), а по оси абсцисс - относительное время (/о = «оО в пределах изменения от О до 4.

Параметры переходных процессов - перерегулирование о(%) и относительное время переходного процесса (Оо4 - для I 1 -/г(/о) =s;0,01 приведены в таблице 5.2.

Хотя приведенные на рис. 5.27 кривые переходных процессов соответствуют л. а. х. типа 2-1 - 2 (рис. 5.14), они с большой степенью точности могут использоваться для оценки переходных процессов в системах регулирования, которым соответствуют симметричные л. а. х. других типов, изображенных, например, на рис. 5.17, 5.19, 5.20, 5.24, 5.25 и 5.26. Для этих л. а. х. характерным является наличие участка с наклоном - 20 дБ/дек в районе пересечения оси абсцисс.

Различие будет наблюдаться в начальной части, если высокочастотная часть данной л. а. х. отличается от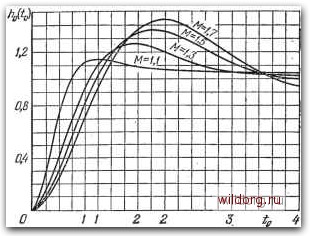

Таблица 5.2

Параметры переходных процессов

Рис, 5.27. Переходные функции систем с типовыми стшетричными л. а. х.

высокочастотной части исходной л. а. х. типа 2-1-2, и в конечной части, если будут отличаться низкочастотные части л. а. х. Таким образом, в случае нужды оценка переходных процессов может осуществляться по универсальным кривым, приведенным на рис. 5.27, во всяком случае для средней части кривой переходного процесса, которая показывает склонность системы к колебаниям и характеризует запас устойчивости.

Можно построить универсальные кривые переходных процессов для случая, когда на вход системы управления поступает сигнал в виде линейной функции g{t) = Vott (t), где го -скорость изменения входной величины. Тогда реакция системы e{t)=g (/) -y{t). может быть записана в виде функции

(-а sin р/о - р cos р + 5-

Здесь коэффициенты Si, а, р. Л, В и С определяются таблицей 5.1. На рис. 5.28 построены универсальные

(-acosP4 + PsinPo) + f:p2]}. (5.176)

О -0J

Рис. 5.28. Ошибки П1)и действии на входе линейно возрастающего сигнала систем с симметричными л. а. х.

кривые для нормированной ошибки Со (о) = i(ifi>oe (о)- Сни являются точными для л. а. х. типа 2-1-2 и прибли-енньми для симметричных л. а. х. других видов, но имеющих типовой переход оси абсцисс (рис. 5.14).

На рис. 5.29 приведены нормированные переходные функции hc(tc) = goy\fo) ДЛЯ систем в которых, исполь-

относительного времени: и,

Wo " шо S f + + (5 sin р/о + с cos В/„) Л„ =