был рассмотрен выше. Эквивалентное значение добротности по ускорению равно

/Са-,. (5.165)

Базовая частота л. а. х. равна

щ = уж2 = уж. (5.166)

Отличие в виде фазовой характеристики в низкочастотной области (рис. 5.25) по сравнению со случаем, изображенным на рис. 5.14, дает некоторый дополнительный запас устойчивости. Как и в предыдущем случае, сильное снижение общего коэффициента усиления может привести к снижению запаса устойчивости и даже к потере устойчивости (при К<.\).

Квазиколебательное звено с отрицательным затуханием. Звено подобного типа имеет передаточную функцию вида

0 (Р) = , 2.„г„р + г?р2 = (-1 +грИЦ-Пр) • • Эквивалентные постоянные времени равны

П = -£оГо-ЬГоКГ+а, (5.168)

т1=1омтоу\+ц. (5.169) Фазовый сдвиг, вносимый звеном, имеет вид

яр = 180° - arctg . (5.170)

Экстремальное значение фазового сдвига получается при со = 7о и равно

я15з = -180°-arctg £о. (5.171)

Как и при квазиколебательном звене с положительным затуханием (5.159), рассматриваемое звено может быть представлено в виде последовательно включенных неустойчивого звена первого порядка (5.150) с постоянной времени То и апериодического звена первого порядка с постоянной времени tq. Однако в данном случае то>Т1, что и дает возможность использовать л. а. х. несимметричного вида (рис. 5.23).

синтез Пас При йеизйёстных характеристиках ггл. 5

Использование л. а. х. симметричного вида здесь не вызывает затруднений, как и в предыдущем случае. Л. а. X. статической системы с объектом рассматриваемого типа полностью совпадает с изображенной на рис. 5.25. Отличие здесь наблюдается только в виде фазовой характеристики в низкочастотной области. Отклонение фазовой характеристики от изображенной на рис. 5.25 пунктирной линии происходит в другую сторону (в сторону больших отрицательных сдвигов).

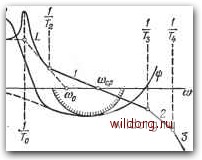Рис. 5.26. Л. а. x. и л. ф. x. статической системы с колебательным звеном, имеющим отрицательное затухание.

Расчет, как и для предыдущего звена, можно свести к расчету системы с астатизмом второго порядка (рис. 5.15). Добротность по ускорению К2 и базовая частота юо определяются приведенньши выше формулами (5.158) и (5.159). Дальнейший расчет производится аналогично изложенному выше.

Колебательное звено с отрицательным затуханием. Звено подобного вида имеет передаточную функцию

o(P) = . 2„U+rgp- (5.172)

Этот случай может быть сведен к системе (5.144). л. а. X. симметричного вида, изображенная на рис. 5.26, полностью совпадает с л. а. х., изображенной на рис. 5.20, а л. ф. X. имеет некоторое отличие. При £о< 1 это отличие наблюдается практически только в низко-

частотной области. Весь расчет аналогичен изложенному выше для звена с передаточной функцией (5.104). Уточненная формула для допустимой суммы постоянных времени совпадает с (5.143), если заменить в ней (To+Ti) на -21лТй- Уточненная формула указывает на некоторое снижение запаса устойчивости по сравнению с системой, имеющей астатизм второго порядка. Однако это снижение обычно невелико, и только в сомнительных случаях (малое значение К или большое значение £о) следует прибегнуть к уточнению расчета.

Переходные процессы в системах с типовыми передаточными функциями. Рассматриваемая ниже методика оценки переходных процессов относится к непрерывным системам. Однако если соблюдать условие того, что частота Т~, где Г -период дискретности, много больше частоты среза л. а. х., то эта методика может быть использована для оценки переходных процессов в цифровых системах управления.

Рассмотрим систему управления, передаточная функция которой в разомкнутом состоянии совпадает с (5.166),

а передаточная функция в замкнутом состоянии имеет вид

"KPJ-x+w (р) TsP+p+ KTp + Ki

Эти передаточные функции соответствуют типовому переходу оси нуля децибел (рис. 5.14), т. е. л. а. х. типа 2-1-2. Воспользовавшись базовой частотой л. а. х.

соо = К-2, можно ввести безразмерное время /о = юо/ и перейти к новой переменной, определяемой соотношением p==cooS. Тогда передаточную функцию (5.173) в нормированном виде можно записать следующим образом:

()=T3s=w.s + l- (5.174)

где Т2 = соо72 и Хз = сооГд - относительные постоянные времени.

Если на вход системы поступает ступенчатый сигнал

g{t)=gol{t), то на выходе системы ее pea кия у (/)