при oiQo (рис.5.21), необходимо выполнение дополнительного условия, которое вытекает из неравенства (5.103):

\W{iqo)\A(qo)<. (5.149)

Выполнение этого условия может быть легко проверено при построении л. а. х. Следовательно, в этом случае появляется запретная зона для л. а. х. в высокочастотной области. Эта запретная зона показана на рис. 5.21.

Для колебательных звеньев со слабым демпфированием (Sol). которое приводит к появлению высокого пика л. а. х., а также для консервативных звеньев (So = 0) наличие такой запретной зоны в

высокочастотной части л. а. х. нежелательно, так как заставляет снижать общий коэффициент усиления. В этих случаях возможно использование л. а. х. с пиком в высокочастотной области, высота которого больше единицы, т. е.

Рис. 5.21. Л. а. x. при наличии высокочастотного колебательного ввена.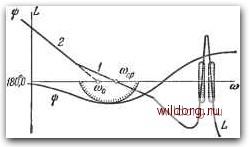

Рис. 5.22. Л. а. х. с дополнительными запретными областями для л. ф. х.

/4(9о)>1- Это показано на рис. 5.22. Однако здесь возникают новые запретные области для л. ф. х. Фазовая характеристика должна обогнуть эти запретные области так. как это показано на рис. 5.22.

Для облегчения выполнения этого условия в канале управления могут применяться звенья, которые дают дополнительные отрицательные фазовые сдвиги в районе частоты соя«(,. Для этой цели, в частности, могут использоваться так называемые неминимальио-фазовые звенья [7, 10].

Системы, содержащие неустойчивые звенья. Канал управления может иметь в своем составе неустойчивое звено. Неустойчивым звеном может быть сам объект управления, либо оно может возникать из-за потери устойчивости по цепи местной обратной связи. Второй случай маловероятен, так как обычно нет смысла выбирать параметры местной обратной связи таким образом, чтобы она была неустойчивой.

Неустойчивый объект первого порядка. В этом случае передаточная функция объекта имеет вид

o(p)=-z:T- (5-150)

Пусть в статической системе управления используется типовая л. а. х. О-1-2-3... (рис. 5.18) и является наибольшей постоянной времени. Передаточная функция разомкнутой системы в этом случае имеет вид

(Р) = ( 1 + т„р)О + т,р)(I + ад...([+ ту (-ISl)

л. а. X. для передаточной функции (5.151) изображена на рис. 5.23. На этом же рисунке изображена л. ф. X. для случая, когда объект устойчив (пунктирная линия), и для случая, когда объект неустойчив (сплошная линия). Из сравнения фазовых характеристик видно, что при выполнении неравенства

Го>соо- = °, (5.152)

которое сводится к условию /<" 1, использование приближенной формулы (5.138) справедливо как для устойчивого, так и для неустойчивого объекта. Однако если в первом случае имелся небольшой дополнительный запас устойчивости, то во втором случае дополнительный запас устойчивости оказывается отрицательным, и в сомнительных случаях при малых значениях общего коэффициента

усиления следует определять запас устойчивости более точно, используя, например, одновременное построение л. а. X. и л. ф. X. (рис. 5.12).

В л. а. X. «симметричного» вида (рис. 5.19) картина получается аналогичной, и при больших значениях общего коэффициента усиления можно пользоваться при-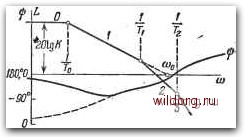

Рис. 5.23. Л. а. x. и л. ф. х. статической системы с неустойчивым звеном первого порядка.

ближенными формулами (5.141) и (5.142). Уточненная формула (5.152) в данном случае приобретает вид

1 = 3

Ум (М-1)

-L.V

м + 1 \ аоТ„ (uoTj М+1 ТоПМ (М-1) (Го- Ti) М

К{М + 1Г

К(М+1)

(5.153)

Заметим, что условие TTi (i = 1, 2, ..., п) является необходимым для получения устойчивой системы. Поэтому при использовании типовой асимптотической л. а. X. (рис. 5.18 или 5.19) ее первый излом должен создаваться постоянной времени неустойчивого объекта.

Неустойчивый объект с передаточной функцией (5.140) в системе с астатизмом первого порядка приводит к более существенным трудностям. Несимметричные л. а. X. типа 1-2-3... (рис. 5.16, б) в этом случае вообще не могут использоваться, так как они дают структурную неустойчивость. Симметричные л. а. х. типа 1-2-1-2-3... (рис 5.17) могут применяться при условии, что Ti является постоянной времени неустойчивого объекта (5.110), т. е. Ti=To. Тогда, если справедливо