до неюугорого предела, который характеризуется минимальными значениями «остаточных» постоянных времени или временных запаздываний, которыми располагает конструктор. Поэтому неизменяемая часть системы определяется здесь в этом смысле.

При построении реальных фильтров возможны следующие случаи.

1. При условии задания характеристик полезного сигнала, помехи, возмущений и неизменяемой части системы требуется найти передаточную функцию системы управления Я (р), при которой обеспечивается выполнение требований по точности, определяемых по среднеквадратичной ошибке, максимальной ошибке, наиболее вероятной ошибке или ИНЫМ образом, и выполняются другие требования к системе, сформулированные в § 4.1.

Задача может облегчаться, если отсутствуют помехи на входе, либо отсутствуют возмущения, приложенные к объекту управления, либо отсутствует и то и другое. Однако она не становится при этом тривиальной.

2. При условии задания характеристик полезного сигнала, помехи, возмущений и неизменяемой части системы требуется определить передаточную функцию системы управления, при которой выполняется условие минимизации дисперсии ошибки М 1еЦ, что соответствует построению оптимальной системы.

Следует обратить внимание на то, что построение реальных фильтров представляет значительно более трудную задачу, чем построение, например, фильтра Винера. В этом можно убедиться, сравнив рис. 4.1 и рис. 4.3. Кроме того, выполнение первой сюрмулированной выше задачи часто оказывается более сложным, чем построение оптимальной системы. Дело заключается в том, что оптимальная система для имеющихся исходных данных всегда может быть построена и трудности нахождения оптимальной передаточной функции Я (р) относятся к чисто математическим. Использование в настоящее время ЭВМ в значительной степени снимает эти трудности. Поэтому задача оптимизации системы управления, например, по минимуму дисперсии ошибки в некоторых случаях приобретает сейчас тривиальный характер.

В то же время задача построения системы с требуемой точностью при имеющихся исходных данных может и не

иметь решения. Если же решить эту задачу все же необходимо, то возможно, что придется решать попутно целый комплекс сложнейших проблем, связанных с переходом к более совершенным элементам системы управления, получением дополнительной информации о входных сигналах системы, например, по первой, второй и более высоким производным задающего воздействия, переходом к более совершенным средствам переработки информации и т. п.

Поэтому первая сформулированная выше задача не теряет своей актуальности, несмотря на развитие теории

оптимальных систем, и, более того, она оказывает сейчас наиболее активное влияние на развитие техники автоматического управления.

При переходе к многомерным системам управления задача построения реальных фильтров сохраняет свое значение. Структурная схема для этого случая изображена на рис. 4.4. На схеме показаны матрицы-столбцы полезных входных воздействий и (t), помех v (t), задающих воздействий g (t), возмущающих воздействий / (t), управляемых величин у (t) и ошибки е (t), а также матрицы передаточных функций Н (р) и Нд (р).

Все приведенные выше соображения по построению непрерывных систем управления на основе использования реальных фильтров практически сохраняют свое значение и для цифровых систем управления с учетом их особенностей - квантования по времени и квантования по уровню.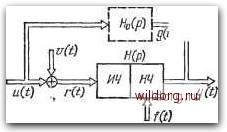

Рис, 4.4. Реальный многомерный фильтр.

§ 4.3. Основы теории фильтров Винера

Как уже отмечалось, задача построения оптимального фильтра Винера (рис. 4.1) относится к категории вариационных задач в открытой области. Уравнение Винера - Хопфа, определяющее оптимальное значение весовой функции замкнутой системы h (t) = j6~ IH (p)], может быть

где корреляционная функция суммарного входного сигнала г (t) = и (О + V (t) может быть записана в виде

/C.Cc) J rit + %)r(%)d% =

= Ки (t) + к. (т) + (т) + Ки-о (т). (4.24)

Взаимная корреляционная функция желаемого выходного сигнала, т. е. задающего воздействия g(i), изображение которого определяется изображением полезного входного сигнала u{t) в виде G(p)=Ho(p)U (р), и суммарного входного сигнала г (t) здесь принята в виде т

Kgrir)= lim \ g(t + x)rit)dt=Kgn{t) + KgAc).

г -00 Jj.

(4.25)

В формуле (4.24) использованы корреляционные функции полезного входного сигнала /<н(т), помехи/С,, (т) и взаимные корреляционные функции полезного сигнала и помехи /Си-в(т) и /Сгр«(т). Этим функциям соответствуют спектральные плотности S„(cu), S.„(cu), S,ro(cu) и Sa{(i), связанные с ними преобразованиями Фурье.

В формуле (4.25) использованы взаимные корреляционные функции полезного сигнала и желаемого значения управляемой величины /Си(г), а также помехи и желаемого значения управляемой величины KgT,{t). Им соответствуют спектральные плотности (со) и Sg, (со). На основании рис. 4.1 можно записать следующие равенства:

5„(ш) = Яо(/ш)5„(ш), (4.26)

S.(«) = 0. (4.27)

В частном случае, когда рассматривается задача оптимальной фильтрации, Но{р) = 1. Тогда Sg.„ (со) = 5„ (со) =

представлено в следующей форме: о

к(%-ц)Кг{п)(1ц, 0<т<сх), (4.23)