Коэффициент гармонической линеаризации

9* = 2 /[«iCOs(f v + 9i)] ехр [-/(-; v + 9i) .

(6.23)

Сложность выражений для коэффициентов гармонической линеаризациии приводит к значительной трудоемкости определения периодических режимов в системе управления с ЦВМ.

Однако при постановке задачи синтеза обычно не ставится вопрос об отыскании периодических режимов.

Наоборот, может быть поставлена задача так синтезировать систему регулирования с ЦВМ, чтобы исключить возможность возникновения периодических режимов в согласованном положении.

Рассмотрим возможность возникновения периодических режимов при использовании типовых л. а. X. симметричного или несимметричного вида (см. § 5.3). Так как мы рассматриваем нормированную нелинейную характеристику преобразователя (рис. 6.2), то коэффициент передачи ЦВМ совместно с входным и выходным преобразователями Лц = бгб будем считать присоединенным к линейной части системы. В работе [128] показано, что для выходных преобразователей с числом разрядов а = 1, а = 2 и а->-оо (в последнем случае статическая характеристика, изображенная на рис. 6.2, соответствует лн-нейной характеристике с насыщением) все возможные годографы величины - Z*(ci, ф1, N) заключены в секторе (рис. 6.4), угол раствора которого y = ziN~.

Периодические режимы в системе будут невозможны, если амплитудно-фазовая характеристика линейной части системы, построенная по функции W {jai) или по функции W*(/?i), на фиксированных частотах алМ (абсолютная частота (x) = nNT~), которым соответствуют фиксированные псевдочастоты (6.7), не будет заходить

Рис. 6.4. Зона расположения годографов нелинейного элемента.

В запретную область. Последняя с запасом может быть представлена в виде сектора с углом y=nN~.

При достаточно больших значениях относительного полупериода Л, т. е. при малых частотах, q* (ах, Фх, Л)->--*-q* («i) и годограф нелинейной части стремится к годографу соответствующей нелинейности в непрерывной системе управления.

Рассмотрим типовые л. а. X. симметричного вида, приведенные на рис. 5.33 и соответствующие использованию непрерывных корректирующих средств. Эти л. а. X. построены на рис. 6.5 совместно с запретными областями для фазовых характеристик, которые определяются сектором, изображенным на рис. 6.4.

Запретные зоны построены относительно фазового сдвига гр = =-180°. Высота запретных зон в угловой мере связана с частотой искомых периодических решений: Q = nN~T~. При = 1 высота запретной зоны равна 180°, при yV = 2 равна 90°, при yV = 3 равна 60° и т. д.

Для исключения периодических режимов фазовая характеристика ф(Я) на фиксированных частотах (6.7)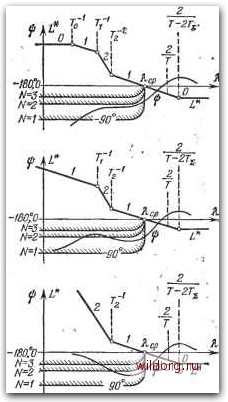

Рис. 6.5. Тииовые л. а. х. симмегрич-ного вида.

1 2 "

(6.24)

не должна заходить в запретные зоны, построенные для

ЭТОГО же значения iV = const. Если фазовая характеристика на фиксированной частоте (6.24) будет находиться в запретной зоне, соответствующей тому же значению N, то возможно существование периодического режима с частотой nN-T~.

Рассмотрим наиболее тяжелый случай астатизма второго порядка (рис. 6.5, в). Условие, при котором фазовая характеристика не будет заходить в соответствующие запретные зоны на фиксированных частотах, имеет вид

-л-Ь<я1,(Х), (6.25)

где %=%1. Формулу (6.25) можно представить в следующем виде:

- л-f - л-f arctg AvTa - 2 arctg -J+

-\-&TCig%N\-Tx). (6.26)

Для частот меньших, чем частота среза {N = = 3, 4, 5, ...), формулу (6.26) с достаточной точностью можно привести к виду

arctg tg-f. (6.27)

Ш-ТШ- (6-28)

Учитывая, что УУЗ, последнее неравенство можно записать в виде

3. (6.29)

Для обеспечения запаса устойчивости в типовой передаточной функции требуется выполнение неравенства

поэтому неравенство (6.29) с запасом выполняется уже при М2. Это же условие получается для типовых передаточных функций с дискретной коррекцией (таблица 5.5).