(5.113)

„ Ti ТАМ-\) 1 УМ(М-\)

3 = -= -д-Г]-----• (5-114)

Формулы (5.113) и (5.114) являются точными, несмотря на то что они получены из асимптотической л. а. х. Это можно проверить, вычислив модуль частотной передаточной функции, соответствующей выражению (5.106), и приравняв частоту значению №„, а модуль -значению YC в соответствии с формулой (5.102):

Отсюда, учитывая, что Ti = hT, h = -j и Ka = Щ, можно получить формулы (5.113) и (5 114).

Приравнивание максимального запаса по фазе р-тах требуемому максимальному запасу по фазе ттах (5.102), в соответствии с рис. 5.14, дает связь между протяженностью участка h и показателем колебательности при оптимальном выборе параметров, т. е. при совпадении максимумов фазовой характеристики и запретной зоны:

Л = §- (5.П1)

М = . (5.112)

Оптимальный выбор параметров здесь означает, что при заданном значении h будет получено минимальное значение показателя колебательности и, наоборот, заданное значение показателя колебательности М получается при минимальной протяженности участка Л.

Л. а. X., которым свойствен типовой переход от нуля децибел в соответствии с рис. 5.14, будем в дальнейшем называть симметричными типовыми л. а. х., имея в виду симметричное расположение фазовой характеристики относительно запретной зоны.

Из рис. 5.14 находятся оптимальные параметры л. а. х.:

«ср м + \-

При равенстве левых частей правым показатель колебательности равен заданному значению М. При неравенстве вводится некоторый дополнительный запас устойчивости и показатель колебательности оказывается меньше заданного значения.

Формула (5.114) также может быть записана в виде неравенства, аналогично (5.116). Однако формулу (5.113) лучше сохранить в виде равенства, так как при фиксированном значении h показатель колебательности будет увеличиваться как при снижении, так и при увеличении Тг-

Учет малых постоянных времени. При использовании передаточной функции вида (5.106) можно ввести дополнительный запас устойчивости с тем, чтобы иметь в канале управления несколько малых постоянных времени, которые можно не учитывать в дальнейших расчетах. Для этой цели можно несколько уменьшить значение постоянной времени Ts, определяемое формулами (5.114) или (5.116), и отодвинуть фазовую характеристику системы от запретной области (рис. 5.15, а).

Обычно достаточно дополнительного запаса по фазе в районе я)) = ijjmax порядка нескольких градусов. Примем, например, что допустимая сумма малых постоянных вре-

Техническая реализация системы тем легче, чем меньше протяженность участка h. Это связано с тем, что введение подобного участка расширяет эквивалентную полосу пропускания разомкнутой системы и повышает уровень высокочастотных помех (которые практически всегда присутствуют во входном сигнале) в h раз. Поэтому с точки зрения оптимальности технического решения необходимо стремиться к тому, чтобы получить желаемый запас устойчивости при минимальном значении h, что и дают приведенные выше формулы.

Вместо базовой частоты соо можно принять, что вся л. а. X. фиксируется заданием частоты среза. Тогда, учитывая, что сОср = ®оТ2, можно получить формулы (5. ИЗ) и (5. И 4) в другом виде:

(5.115)

(5.116)

мени, которые можно не учитывать в расчете, составляет

«о

(5.117)

при числе малых постоянных времени, равном 4-г-6. Тогда граница малых постоянных времени определяется величиной

0,025

(5.118)

Если в этом случае некоторая малая постоянная времени дает сопрягающую частоту

со„ = Т„->сОг = 7г. то ее можно не учитывать при расчете при условии, что число таких постоянных времени не превосходит. 4-5-6.

При введении дополнительного запаса устойчивости расчетная формула (5.113) сохраняется , а формула (5.114) приобретает вид

Ум (М -1)

М + 1 \

-0,1 . (5.119)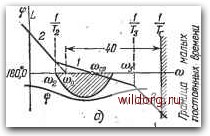

Рис. 5.15. Л. a. x. систем с астатизмом второго порядка (тип 2-1-2 и тип 2-1-2-3).

Л. а. X. типа 2-1 - 1-3 - 4... В этом случае передаточная функция разомкнутой системы имеет вид

W{P):

KA + TiP)

f(\+Tp)(\+T){\ + T,p) ... (\+Т„р) •

(5.120)

Число множителей типа (1+Т<р) в знаменателе не ограничено, т. е. может рассматриваться система любого порядка. Л. а. X. изображена на рис. 5.15,6. Наклоны асимптот имеют значения -2-20 дБ/дек, -1-20 дБ/дек, -2-20 дБ/дек, -3-20 дБ/дек и т. д. до значения (я - 1) -20 дБ/дек. Для получения заданного показателя