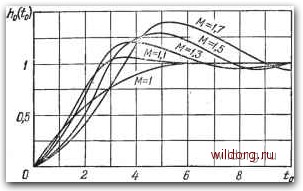Рис. 5.29. Переходные функции систем с типовыми несимметричнынш п. а. х.

время в этом случае to = (i)ot. По оси ординат на графике переходных функций отложена величина ho(io) = g»y {(nj).

На рис. 5.30 приведены нормированные кривые ошибок в функции относительного времени 1о = щ1 для систем с несимметричными л. а. х. при поступлении на вход системы сигнала g{t) = vj:\ (t). На оси ординат отложена величина eo{to) = e {Qley„. Установившаяся ошибка определяется выражением

(5.177)

где «о = /<! -базовая частота л. а. х. (рис. 5.16). Пользоваться этими кривыми можно так же, как и кривыми рис. 5.29.

Можно показать [7], что рассмотренные типовые передаточные функции близки к оптимальным при необходи-

зуются несимметричные л. а. х., изображенные на рис. 5.16, 5.18 и 5.23. За исходную принята л. а. х. типа 1-2, для которой эти кривые являются точными. Если показатель колебательности не превышает значения 1, 3, то этими кривыми можно пользоваться и в случае использования л. а. X. других типов.

В качестве базовой частоты «о в л. а. х. несимметричного типа используется частота пересечения асимптоты с наклоном -20 дБ/дек и оси абсцисс. Относительное

МОСТИ обеспечить воспроизведение полезного сигнала (задающего воздействия) с требуемой точностью и при

Во i

Рис. 5.30. Ошибка при действии на входе линейно возрастающ,его сигнала систем с несимметричными л. а. x.

выполнении условия минимизации полосы пропускания разомкнутой системы, т. е. в смысле минимизации функционала (4.2).

§ 5.4. Типовые передаточные функции цифровых систем управления

В цифровых системах возможно использование рассмотренных в предыдущем параграфе типовых л. а. х. (типовых передаточных функций) при учете особенностей, которые вносятся дискретностью.

Выбор низкочастотной части л. а. х. должен делаться в соответствии с методикой обеспечения заданной точности, изложенной в § 5.3. Для этого необходимо, чтобы л. а. X. не заходила бы в запретную область, форма которой определяется заданием дисперсий (или максимальных значений) входного сигнала и его производных, а также дисперсий (или максимальным значением) ошибки воспроизведения. При этом предполагается, что для частот, которые определяют расположение запретной области

g B.4J Типовые передаточные функции цас 4lt

по точности, справедливо утверждение о практическом совпадении круговой частоты с псевдочастотой, т. е.

X=-arctg(o. (5.178)

Условие (5.178) определяет понятие низких частот в рассматриваемой системе.

Построение средне- и высокочастотной частей желаемой типовой л. а. X. производится в соответствии с изложенным, но с учетом особенностей построения л. а. х. цифровых систем, которые были изложены в главе 2. Эти особенности сводятся к методике учета малых постоянных времени и к учету эффекта транспонирования частот в колебательных и консервативных звеньях.

Типовые передаточные функции цифровых систем при использовании непрерывных корректирующих звеньев. Рассмотрим методику построения типовой л. а. х. для цифровой системы при использовании экстраполятора нулевого порядка. Пусть асимптотическая л. а. х. непрерывной системы, удовлетворяющей требованиям точности воспроизведения задающего воздействия и требованиям по запасу устойчивости, имеет вид, изображенный на рис. 5.31, а. Изломы асимптотической л. а. х. определяются реальными постоянными времени апериодических звеньев, входящих в структуру системы (объект, исполнительные элементы, усилители и др.), и постоянными времени используемых в системе непрерывных корректирующих звеньев.

Выберем некоторое значение периода дискретности Т и проведем на логарифмической сетке вертикальную прямую на частоте 27"-. Тогда на основании изложенного в § 2.8 вся асимптотическая л. а. х. непрерывной системы левее частоты со = 27"- перейдет в асимптотическую л. а. х. цифровой системы. Область частот от правого края запретной области по точности до частоты (u = 27-i представляет собой область средних частот. Таким образом, и в области низких частот (в районе запретной области по точности), и в области средних частот построение л. а. x. цифровой системы не имеет никаких особенностей по сравнению с непрерывной системой (рис. 5.31, б).

Из изложенного в § 2.8 следует, что правее частоты (О = 27 1, т. е.. в области высоких частот, асимптотическая