сона (треугольный закон распределения). При действии i преобразователей суммарная дисперсия равна i/l2. При этом закон распределения будет тем ближе к нормальному, чем больше число L

Приближенное значение дисперсии шумов квантования на выходе ЦВМ может быть определено из выражения

*(А) \dX

(6.131)

Вместо приближенной формулы (6.131) можно воспользоваться точными формулами, приведенными в § 3.7, что вызывает, однако,

Inrn

усложнение расчетов. При числе t > 1 и сравнительно большом числе членов передаточной функции D{z) для процесса на выходе ЦВМ можно принять нормальное распределение. Тогда влияние шумов квантования можно учесть следующим образом. Пусть система находится в режиме, когда требуется обеспечивать максимальное управление Xio (рис. 6.23). На этот режим накладываются шумы с дисперсией При этом результирующий сигнал на выходе ЦВМ может попадать как на наклонный участок линеаризованной характеристики, так и на участки насыщения.

Считая, что для сигналов в цифровой (относительной) форме коэффициент передачи на наклонном участке равен единице, а на участках насыщения равен нулю, можем представить результирующий коэффициент передачи в виде

kpP{-x,-Xio<x<x,-Xio), (6.132)

где вероятность нахождения шумового сигнала х на наклонном участке характеристики (рис. 6.23), равная

Рис. 6.32. Пример статической характеристики выходного преобразователя.

результирующему коэффициенту передачи, определяется интегралом вероятностей

- %0

(6.133)

При известных значениях а„ и можно подобрать такое значение х„, пользуясь формулой (6.135), при котором снижение общего коэффициента усиления оказывается допустимым. Заметим, что при выборе а = ао, т. е. при Xn = >x(i, формула (6.133) дает

(6.134)

что соответствует возможному снижению общего коэффициента усиления более чем в два раза.

Определим, например, снижение общего коэффициента усиления при выборе выходного преобразователя в соответствии с рис. 6.23 для рассмотренного выше примера 6.3 в случае наличия двух входных преобразователей. В соответствии с формулой (6.131)

i 12 2л

1 + }Кх 2 dX

-L(\ .11= L± 2 14-0,922 24 7/ 12(1 -а)2 12(1-0,92)2

Среднеквадратичное значение o

муле (6.133) находим при Xio = 3 и x=7

12(1-0,92)2 7. Далее по фор-

Кр- 2

1\о\

-f Ф()] = у (0,847-f 0,431) = 0,639.

Относительное снижение общего коэффициента усиления составляет здесь 36,1%, что в некоторых случаях может быть недопустимым и требует увеличения зоны линейности, т. е. значения а.

Снижение требований к расширению зоны линейности, т. е. снижение требуемого количества дополнительных разрядов в выходном преобразователе, может быть достпг-руто уменьшением цены единицы младшего разряда вход-

НОГО и, соответственно, выходного преобразователей, что увеличивает число ступенек в нелинейной характеристике преобразователя (рис. 6.23) и снижает эффект действия шумового процесса на выходе, поскольку величина остается неизменной при неизменной передаточной функции. Так, для рассмотренного примера, если уменьшить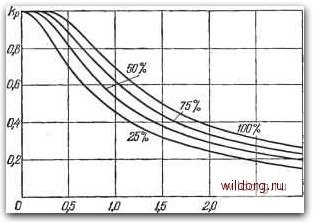

Рис. 6.24. Нормированные кривые подавления коэффициента усиления шумами квантования.

вдвое цены единиц младшего разряда на входе и выходе, то «0 = 3 и а = 4. Тогда при Xio = 7 и х„ = \Ь

Ф () -f Ф (I)] = I (0,998 + 0,746) = 0,872.

В этом случае снижение коэффициента усиления составляет только 12,8% при относительно меньшем расширении зоны линейности преобразователя.

На рис. 6.24 построены нормированные кривые для определения результирующего коэффициента передачи ЦВМ при различных уровнях шума квантования и различных запасах линейности выходного преобразователя. Запас линейности дан в относительных единицах {х - Хю) для значений 25%, 50%, 75% и 100%. Значение 100% соответствует случаю отсутствия установившегося значения управления, т. е. при a:io = Q,