Спектральная плотность ошибки

;со<рг). (6.22)

Дисперсия ошибки в рассматриваемой системе D.= ldco=(arctg-arctg). (Б.23)

Так как arctgA;l<;lA;l, то из последнего равенства вытекает условие

(5.24)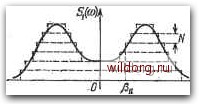

Таким образом, при любых значениях Pi и Рг дисперсия ошибки в выбранной системе управления не превышает заданного значения. Только в предельном случае, когда pi- -Р и P2-Pi, что соответствует случаю гармонического входного сигнала, получается условие De-De.

Аналогичный пример может быть рассмотрен и для дискретного случая при условии выполнения неравенств Pi-T" и Ра < Т-, где Т - период дискретности.

Покажем теперь, что полученный результат можно распространить на спектральную плотность Si(©) любого вида. На рис. 5.4 изображена спектральная плотность Si (со) произвольного вида, приближенно представляемая в виде совокупности равномерных спектров высотой и протяженно-тью от ± Pi; до ± Рг;, где г = 1, 2, ..., я. Д Персия скорости для совокупности равномерных спект-i-oa

Рис. 5.4. Замена прозвольной спектральной плотности суммой равномерных спектров.

(5.25)

Дисперсия ускорения

Действительная дисперсия ошибки системы при действии совокупности равномерных спектров в соответствии с (5.23) будет

D=ii(-tg%-arctg-). (5.27)

Отсюда следует:

При бесконечном уменьшении высоты равномерных спектров и при одновременном бесконечном увеличении их числа можно аппроксимировать исходную спектральную плотность Si (со) с любой степенью точности. Следовательно, доказано условие того, что действительная дисперсия ошибки DeD*, будет справедливо при любом виде спектральной плотности Si (со), но при ограниченных значениях Di и Da.

Усложним теперь передаточную функцию системы в разомкнутом состоянии и представим ее в виде

Выполним условие достаточно большого запаса устойчивости в замкнутой системе. Примем, например, что корни характеристического уравнения замкнутой системы

Тгр + Р + Ki = Ki (1 + Tip) (1 + Tap) = О (5.30)

являются вещественными отрицательными. Это будет при выполнении неравенства Ti<0,25Ki. Выберем общий коэффициент усиления разомкнутой системы в соответствии с формулой (5.17). Л. а. х. разомкнутой системы изображена на рис. 5.5, а. Найдем действительную диспер-

СИЮ ошибки в системе с передаточной функцией (5.29); 1 f N (l+orf) da

i ( 1

. (5.31)

Здесь Ti и Тг - постоянные времени, определяемые корнями характеристического уравнения замкнутой системы: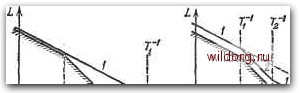

Рис. 5.5. Расположение низкочастотной части л. а. х. относительно запретной области по точности.

%г - - и Т2 = - Ра. Коэффициенты разложения на простые дроби

Л, =

х\-Т\

т2 т2

Ti - Та

(5.32)

Из (5.32) следует, что если принять Ti>-T2, то минимальное значение т"" = 0,5/(i. Поэтому Л1>0. Должно выполняться условие Лд + Лг = 1, а коэффициент Л 2 может быть как отрицательным, так и положительным. Проинтегрировав (5.31), получим

-А (arctg paTi - arctg PiTi) +

-1- - (arctg - arctg pjXz)

(5.33)