На основании (2.136) дискретная передаточная функция разомкнутой системы в области низких частот

knT г+1

г+1 у/у/- , V Ni(l~di) 2 (z-lf -т- г-1 " L г-di

~ 2 (г-1)2+ г-1 + Zj г-rff • (-0

где /С = „6А -общий коэффициент передачи непрерывной части с учетом преобразователей, а di = e~i (i=l, .... 9).

Перейдем к дискретной частотной передаточной функции заменой z на ш по (2.187) и © = /0,577,. В результате получим

2

(2.218)

Так как было принято, что Ti>Q,bT, то

откуда получаем

n7g„(/?.)(l-Af

(2.219)

Сравнение последнего выражения с (2.215) показывает, что частотные передаточные функции ШонЦЦ и W„(/u)) в низкочастотной области совпадают с точностью до множителя 6/61. Так как было принято, что а>Т<.2, то влия-

(т\ 1 -/X-g- в (2.219) можно

не учитывать при построении л. а. х. в низкочастотной области.

Совпадение логарифмических частотных характеристик для дискретной передаточной функции и для исходной передаточной функции непрерывной части в области

низких частот дает большие удобства в формировании низкочастотной части л. а. х. проектируемой системы и позволяет ориентироваться на методику, используемую для непрерывных систем.

Рассмотрим построение логарифмических частотных характеристик в области высоких частот при coTl. Введем следующие ограничения.

1. Величина, обратная периоду дискретности Т, больше половины частоты среза л. а. х. непрерывной части системы, т. е. сО(.рТ<2. При расчете систем с ЦВМ это неравенство приходится выполнять практически во всех случаях в связи с требованиями по устойчивости и запасу устойчивости.

2. Если рассматривать передаточную функцию непрерывной части в виде

„(Р)=-Г-. (2-220)

РП(1-ЬГ,р) »=1

где К = kjslbi [с-] - общий коэффициент усиления, а г - степень астатизма, то все постоянные времени Ti, ..., Т„ можно разделить на две группы. К первой группе, Ти Тд, отнесем те из них, которым соответствуют сопрягающие частоты меньше 27" (большие постоянные времени). Они участвуют в формировании низкочастотной части логарифмических характеристик в соответствии с изложенным выше.

Ко второй группе, T+i, Тп, отнесем те постоянные времени, которым соответствуют сопрягающие частоты, большие чем 27 (малые постоянные времени), причем для каждой постоянной времени второй группы должно выполнятся неравенство Ti<.0,bT (t = 9-1-1, п). Случай комплексных полюсов (2.220) рассмотрим ниже отдельно.

3. Постоянным времени Ti, ..., соответствуют сопрягающие частоты, меньшие частоты 2Т~, и они участвуют в формировании низкочастотной части логарифмических характеристик. Это требование не относится к тем постоянным времени числителя (2.220), которые были введены для компенсации в непрерывной части некоторых полюсов

передаточной функции и поэтому после сокращения одинаковых множителей не вошли в окончательное выражение (2.220).

4. Пересечение вертикальной прямой со==2Г- асимптотической л. а. X. непрерывной части происходит при отрицательных наклонах 20 дБ/дек и 40 дБ/дек. Эти случаи будут рассмотрены отдельно.

Область Высоких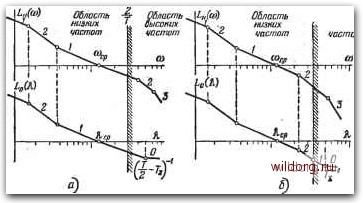

Рис. 2.28. Л. а. х. непрерывной части ЦАС с экстраполятором нулевого порядка.

Рассмотрим сначала случай, когда пересечение вертикальной ЛИНИЙ со = 2Т~ асимптотической л. а. х. непрерывной части происходит при отрицательном наклоне 20 дБ/дек (рис. 2.28, а). Тогда в области высоких частот (со>2Т~) передаточная функция непрерывной части может быть представлена в виде

WbW р(1+Г5«р)...(1+г„р)-

(2.221)

Здесь соов представляет собой базовую частоту высокочастотной части л. а. х., определяемую как частота пересечения ее первой асимптоты с осью нуля децибел. Базовая частота определяется выражением

fCTiTa...Tm

(2.222)

причем должно выполняться, условие mq + r-l.