Дальнейший расчет близок к изложенному выше для случая, изображенного на рис. 3.10, а. Разница будет заключаться в том, что для воздействия Д должна использоваться та же передаточная функция Не (е">) или Щ (/Я,), которая справедлива для задающего воздействия.

Рассмотрим только случай отсутствия корреляционной связи между g и Д. Тогда спектральная плотность ошибки

S* {%) = I т (/Я) i" [S (Я) + St{-k)]. (3.123)

Далее по формуле (3.118) может быть найдена дисперсия ошибки Dg.

§ 3.7. Приближенный расчет

дополнительных ошибок ЦАС, вызванных квантованием по уровню

При рассмотрении типовых случайных процессов в § 3.4 был введен дискретный белый шум, генерируемый устройствами квантования по уровню (округления) в ЦАС. Источниками такого шума могут быть входные и выходные преобразователи ЦАС. Кроме того, процессы округления могут наблюдаться в арифметическом устройстве ЦВМ при реализации дискретных алгоритмов коррекции ЦАС. Более строго вопрос учета шумов квантования будет рассмотрен ниже в 3.8.

Линейный дискретный корректирующий алгоритм ЦВМ может представляться либо в виде передаточной функции (2.155), либо в виде разностного уравнения (2.156). Положив «0=1, что всегда можно сделать, запишем передаточную функцию в виде

Этой передаточной функции соответствует разностное уравнение

x[n\ = boe[n\-\-bie[n-l]-f ... -\-bke[n-k]-

-{аМп-Ц + агх[п-2-]+...+ ах[п-Щ). (3.125)

Структурная схема реализации алгоритма, заданного передаточной функцией (3.124) и разностным уравнением (3.125), изображена на рис. 3.11. На схеме введены квантователи К, соответствующие округлению в арифме-

тическом устройстве ЦВМ, квантователь Ki входного преобразователя и /Сг выходного преобразователя. Импульсные элементы, работающие с переходом Т, показаны только на входе и выходе структурной схемы и не показаны внутри структурной схемы, где они должны были бы иллюстрировать порядок производства операций в арифметическом устройстве.

/Г, 7-

г>-<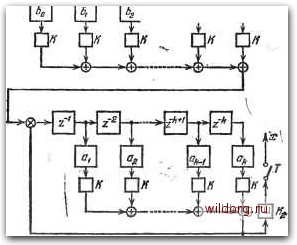

Рис. 3.11. Структурная схема реализации линейного корректирующего алгоритма в ЦВМ.

Схема, изображенная на рис. 3.11, соответствует так называемому прямому программированию при реализации передаточной функции (3.125) или ей соответствующего разностного уравнения (3.124). Другие подходы при их реализации будут рассмотрены ниже в § 5.5.

Так как число разрядов арифметического устройства выше числа разрядов входного преобразователя, то цифровая единица младшего разряда входного преобразователя содержит 2У цифровых единиц арифметического устройства, где у -целое число (обычно у = 3 - 4).

Если использовать изложенный выше прием замены эффекта квантования дискретным белым ш)тмом (рис. 3.6), то структурная схема реализации линейного алгоритма ЦВМ может быть сведена к виду, изображенному на рис. 3.12. Здесь Vi представляет собой дискретный белый шум, который генерируется входным преобразователем. Он вводится в ЦВМ с коэффициентом передачи бг, если его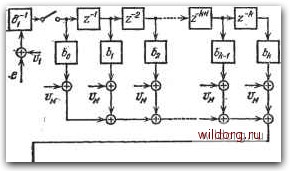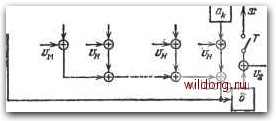

Рис. 3.12. Преобразованная структурная схема реали-вации линейного корректирующего алгоритма в ЦВМ.

рассматривать отнесенным ко входу ЦВМ. Коэффициент передачи будет равен единице, если рассматривать шум, приложенный ко входу преобразователя.

При рассмотрении шума, генерируемого входным преобразователем, возможны два случая. В системах стабилизации задающее воздействие g=0. Поэтому шум генерируется только преобразователем, осуществляющим ввод в ЦВМ управляемой величины у (рис. 1.3). В этом случае корреляционная функция шума Vi на входе входного