2 = il/7M~T \ т т VM(M-1)

или в соответствии с формулами (5.115) и (5.122)

< = 3

СОср м + 1-

При более точном расчете можно учесть дополнительный запас по фазе (по сравнению с системой, имеющей астатизм второго порядка)

Д(х = arctg(5.130)

Это обстоятельство позволяет немного увеличить допустимую сумму постоянных времени Т, определяемую формулами (5.120) или (5.121), или немного уменьшить требуемое значение постоянной времени Га, определяемое формулами (5.113) или (5.115). Первое обычно бывает более предпочтительным. В результате могут быть получены уточненные формулы для допустимой суммы

фазе. Это будет тем справедливей, чем больше необходимое значение добротности по скорости. Поэтому с большой степенью точности здесь могут быть использованы формулы предыдущего параграфа, дающие связь между общим коэффициентом усиления Ki, показателем колебательности М и постоянными времени для случая астатизма второго порядка.

В рассматриваемом здесь случае положение всей л. а. х. определяется значением базовой частоты (рис. 5.17)

(Оо = Т/Га = ]/-. (5.129)

В соответствии с формулами (5.113) и (5.121) имеем

ПОСТОЯННЫХ времени:

27=i

(Ym{m-\) 1

«ср

, (5.131)

ЖТГ + Л)- (5-132)

При этом постоянная времени по-прежнему определяется формулами (5.113) или (5.115). Однако уточнение, даваемое формулами (5.131) и (5.132), обычно не имеет практического значения, и расчет можно вести по формулам (5.120) или (5.121), которые были получены для системы с астатизмом второго порядка.

Статические системы. Статические системы обычно получаются при регулировании различных производственных объектов, при регулировании скорости вращения двигателей и при управлении усилителями с глубокой обратной связью (например, операционными). В простейшем случае передаточная функция разомкнутой статической системы имеет вид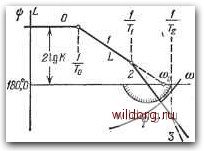

Рис. 5.18. «Несимметричная» л. а. X. статической системы (тип 0-1-2- 3...).

(Р)- (\ + Т,р){\+Тф)

(5.133)

где /С -общий коэффициент усиления, 7"о - наибольшая постоянная времени (обычно объекта регулирования), Ti - постоянная времени, определяемая обычно инерционностью канала управления. Соответствующая асимптотическая «несимметричная» л. а. х. типа 0-1-2... изображена на рис. 5.18 сплошной линией.

При больших значениях общего коэффициента усиления передаточная функция в районе пересечения л. а. х. оси нуля децибел (в этой области частот) может быть приближенно сведена к передаточной функции системы с

(5.136)

Для передаточной функции более сложного вида К

W(p) = .

П i + Tip)

(l + ToP)(l+T,p){l + TiP) ... Ц + Т) аналогично (5.127), имеем

(5.137)

(5.138)

Последнее выражение дает достаточно точные результаты при М1,3.

Из выражений (5.136) и (5.138) видна роль первой большой постоянной времени Го как фактора, увеличивающего запас устойчивости системы. Повышение общего коэффициента усиления или повышение значения суммы остальных постоянных времени при заданном запасе устойчивости может быть сделано при увеличении постоянной времени 7"о.

Отклонение передаточной функции (5.134) в области низких частот от ее точного выражения (5.133) приводит, в результате использования расчетных формул (5.136) или (5.138), к некоторому дополнительному запасу устойчивости. Однако учет этого обстоятельства обычно делать нецелесообразно ввиду его незначительности [7].

астатизмом первого порядка

где базовая частота л. а. х. равна

соо = #. (5.135)

Это дает возможность использовать полученную выше для л. а. X. типа 1-2 формулу (5.125) при замене Ki на КТ. Тогда условие получения заданного запаса устойчивости имеет вид