синтез цас При неизвестных характеристиках [гл 6

Дискретная передаточная функция имеет вид Дискретная частетная передаточная функция -

(5.227)

Соответствующая л. а. х. L* (К) построена на рис. 5.42.

Примем в качестве желаемой л. а. х. L«<i, изображенную на рис. 5.42. Она соответствует передаточной функции (см. таблицу 5.3 и рис. 5.33) разомкнутой системы

W*,(A) =

(5.228)

при условии, что Ti = 0, где t = 3, 4, п. Дискретная частотная передаточная функция последовательного корректирующего устройства имеет вид

iSk(A)= = i + №.

Переход к передаточной функции ЦВМ дает

(5.229)

(5.230)

Последнее выражение определяет неустойчивую программу, так как полюс передаточной функции Zi = -1

соответствует колебатель-JAwj ной границе устойчивости.

Заметим, что получившаяся частотная передаточная функция корректирующего устройства (5.229) не может быть реализована, вообще говоря, и в непрерывном варианте. Эта функция соответствует бесконечному подъему усиления при росте частоты до бесконечности. При реализации в дискретном варианте эта функция приводит к неустойчивой программе ЦВМ. Для исключения этого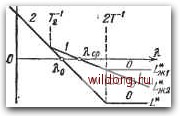

Рис. 5.42. Варианты выбора желаемой л. а. X.

(A)«(i+A J)

соответствует типовой функции в таблице 5.5. Передаточная функция корректирующего устройства в этом случае имеет вид

;5к(/Я) = = 1±. (5.232)

Переход к передаточной функции ЦВМ дает

(г) = D (z) - = . (5.233)

где а = {2Т2 - Т) (27 + Т)-. Этой передаточной функции соответствует устойчивая программа ЦВМ.

Для рассмотренного примера произведем числовой расчет. Пусть по условиям точности /Сг = 100 с-2, а показатель колебательности Л4 = 1,5. Дальнейший расчет произведем в соответствии с формулами (5.115) и (5.116). Базовая частота л. а. х.

Яо = 1 С2= 1100= 10 с-1. Требуемое значение постоянной времени равно

Допустимое значение суммы малых постоянных времени для передаточной функции (5.231) равно периоду дискретности:

22~-Ко М + \ 10 1,5+1 и.шадс.

Примем период дискретности Т == 0,0346 с. Передаточная функция ЦВМ (5.233) имеет вид

Л ,2-0,173\ 2-0,173

D (г) = I + 0.0346 0.0346 оз2,-х).

явления примем желаемую л. а. х. 1ж2 в другом виде (рис. 5.42). Желаемая передаточная функция

2 (А) =-, г\ (5-231)

СИНТЕЗ ЦЛС ПРИ НЕИЗВЕСТНЫХ ХЛРЛКТЕРИСТИКЛХ [ГЛ. 5

Множитель 5,5 может быть присоединен к непрерывной части.

В таблице 5.8 приведены некоторые простейшие дискретные корректирующие средства, которые могут реализоваться на ЦВМ или дискретных фильтрах. Переходные характеристики в таблице 5.8 построены для случая использования экстраполятора нулевого порядка.

В самом общем случае передаточная функция корректирующего устройства имеет вид

0{г)

Ьр+Ьг- + .-. + Ьг-" б(г)

l+fl.i2-i + ...+fl,,z-i l+A(z)

(5.234)

Эта передаточная функция соответствует так называемому рекурсивному фильтру. Если А (г) = О, то будет получен нерекурсивный фильтр.

--------->©

Рис. 5.43. Первая каЕ0ЕИчес1гая схема дискретного фильтра.

Структурная схема реализации на ЦВМ передаточной функции (5.234) была приведена на рис. 3.12. Она соответствует так называемому прямому программированию. Как следует из структурной схемы, при реализации ее не на ЦВМ, а в виде отдельного дискретного фильтра, требуется 2k линий задержки.

Более экономными в этом смысле оказываются канонические схемы дискретного фильтра. Первая форма канонической схемы, к которой может быть преобразована схема прямого программирования, изображена на рис. 5.43. Она содержит только k линий задержки. В отличие от исходной схемы (рис. 3.12), на ней не