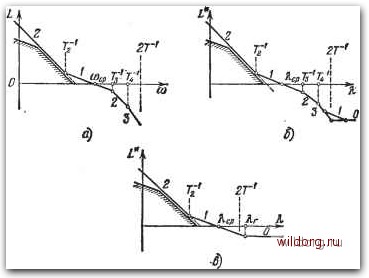Рис. 5.31. Переход от л. а. х. непрерывной системы к дискретной.

Ход л. а. X. в высокочастотной области и тот или иной вид сопряжения последней асимптоты со средне-частотной частью л. а. х. не имеют практического значения. Важно, чтобы вид л. а. х. правее частоты среза (й(.р?5аЯср отвечал бы условию ограничения суммы малых постоянных времени в соответствии с формулами § 5.3. Кроме того, должно быть наложено ограничение на высоту резонансных пиков в области высоких частот, если фазовый сдвиг, который имеет система без учета рассматриваемого колебательного звена, в районе пика лежит в пределах 0<il)<-f 180°.

Таким образом, в цифровых системах с экстраполятором нулевого порядка эквивалентная постоянная времени, которая должна учитываться в формуле для малых

Л. а. X. цифровой системы имеет последнюю асимптоту с нулевым наклоном. Сопряжение этой асимптоты со среднечастотной частью может быть различным, что показано на рис. 5.31, б в виде некоторой области сопряжения.

fi 541

типовые передаточные функции цас

постоянных времени, равна

(5.179)

где Гц -сумма малых постоянных времени непрерывной части системы, х < Г - временное запаздывание.

Кроме того, должно проверяться отсутствие захода л а X при Я,>Я,г в область, ограниченную прямой L* = 20 Ig М (М + 1)-1 (рис. 5.32).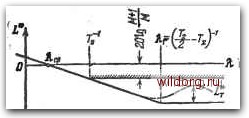

Рис. 5.32. К построению высокочастотной части л. а. х.

В цифровых системах с экстраполятором первого порядка вместо (5.179) должна рассматриваться формула

Г, = 72 +т. (5.180)

Изложенное позволяет сформулировать требования к типовым передаточным функциям разомкнутой цифровой системы. Выполнение этих требований гарантирует получение заданного запаса устойчивости. В низкочастотной и среднечастотной областях л. а х. цифровой системы должна совпадать с какой-либо типовой л. а. х. «симметричного» или «несимметричного» вида из рассмотренных в § 5.3. Высокочастотная часть л. а. х. должна удовлетворять требованиям по ограничению суммы малых поегоянных времени.

В соответствии с классификацией типовых л. а. х., приведенной в § 5.3, для статических систем здесь будут получаться л. а. х. типа О-1-2-1-3...О, для систем с астатиамом первого порядка -л. а. х. типа 1-2-1-3... ...О и для систем с астатизмом второго порядка -л. а, х. типа 2-1-2-3...U.

Так как практически во всех случаях целесообразно иметь в цифровой системе наибольшее допустимое значение периода дискретности, то вертикальную линию на частоте (0 = 27-1 следует стремиться расположить на асимптоте единичного наклона правее частоты среза (рис. 5.31, в).

В таблице 5.3 приведены типовые передаточные функции разомкнутых цифровых систем с экстраполяторами нулевого порядка, которым соответствует л. а. х. «симметричного» вида, для запаздывания т = 0 и при выполнении условия максимизации периода дискретности.

Отказ от последнего условия позволяет иметь в знаменателе передаточной функции дополнительные множители типа {l--jlTi) при ограничении суммы постояниых времени в соответствии с формулой (5.179) либо дополнительные множители, соответствующие колебательным звеньям при ограничении суммы постоянных времени и высоты резонансных пиков.

Кроме того, принято, что постоянные времени удовлетворяют условиям: То>0,5Т, Г1>0,5Т, Та > 0,57 и Tj<0,5T, где t = 3, 4, /г. Это означает, что вертикальная прямая <в = 2Т- пересекает асимптоту л. а. х., имеющую наклон 20 дБ/дек. Таблица 5.4 соответствует таким же передаточным функциям цифровых систем, но с использованием экстраполяторов первого порядка.

Асимптотические л. а. х., соответствующие типовым передаточным функциям таблиц 5.3 и 5.4, изображены на рис. 5.33. На рис. 5.33, а изображены л. а. х., соответствующие дискретной частотной передаточной функции, а на рис. 5.33, б-соответствуюише исходной передаточной функции непрерывной части. Граничная частота К для цифровых систем с экстраполятором нулевого порядка

равна .г = (-2 - Ти] ; для цифровых систем с экстраполятором первого порядка - (Г - Т-)-. В соответствии с классификацией, принятой в § 5.3, здесь для статических систем получаются л. а. х. типа 0 - 1-2-1-0, для систем с астатизмом первого порядка -л. а. х. типа 1 2 ~ 1 - О и для систем с астатизмом второго порядка-л. а. X. типа 2-1-0.