Пересчет этой передаточной функции на передаточную функцию последовательного звена (5.249) дает

D* ЦК) =

Передаточная функция разомкнутой системы использовании принятого значения В* (jX)

lF*(A) = D*()lFg(A)-

Ориентировочное значение эквивалентной суммы малых постоянных времени здесь оказывается равным ТТ, что совпадает со случаем использования последовательного

корректирующего звена.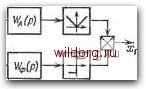

Рис. 5.45. Псевдолинейное корректирующее звено.

Это говорит о возможности использования уточненной передаточной функции В (г) вместо исходной Bo(z). При необходимости может быть сделан более точный расчет с построением л. а. х. и л. ф. X. для полученной передаточной функции W* (jK).

Псевдолинейные корректирующие устройства. Теория использования нелинейных корректирующих устройств наиболее полно разработана в настоящее время для так называемых псевдолинейных устройств, характеристики которых не зависят от амплитуды входного гармонического сигнала. Это делает их похожими на линейные звенья. Вместе с тем они позволяют формировать отдельно амплитудную и фазовую частотные характеристики устройства, что невозможно для линейных систем.

Структурная схема псевдолинейного устройства изображена на рис. 5.45. Верхний канал содержит элемент взятия модуля, а нижний - элемент определения знака сигнала.

В верхний канал введено звено формирования амплитудной характеристики с передаточной функцией W{p),

а нижний канал -звено формирования фазовой характеристики с передаточной функцией И?ф(р). Выходной сигнал получается перемножением сигналов двух каналов устройства.

Исследование подобного устройства проще всего можно провести посредством использования метода гармонической линеаризации [79]. Коэффициенты гармонической линеаризации при выполнении условий для фазовых сдвигов фазового и амплитудного каналов

0=Ффя, -яФО, я -ффФа (5.250) должны определяться в соответствии с выражениями

4 = \Wa (/«) [(4 - I Фа I - Фф) COS ф, + sin I ф J +

Н-8ШффС08(ф, + фф)], (5.251)

q = i\Wa (/со) I [( - 4 + 1 Фа I + фф) sin I Фа I +

+ 5Шфф8ш(фЛ-фф) . (5.252)

При выполнении условий

ОффЯ, -ЯфаО, -Я-фффа

- в соответствии с выражениями

?=~- Wa(i(i>)\ (-п +фа + фф)с08фа-5Шфа-

-8ШффС08(фа + фф)

«7 - I (т [( - I Фа 1 - фф) sin I Фа I --5Шфф8Ш (фa-f фф)

(5.253)

(5.254)

Приведенные формулы соответствуют наиболее важному случаю, когда амплитудный канал создает подавление сигнала и вводит отрицательные фазовые сдвиги, а фазовый канал дает фазовое упреждение. Это позволяет получать необходимые запасы устойчивости в замкнутой системе при амплитудном подавлении сигнала.

Можно показать [79], что для приближенных представлений амплитудной и фазовой характеристик псевдолиней-

НОГО устройства допустимо использовать приближенные формулы

1 "п. (/co)i = уфМШШ 1 т\ X

X [0,64 + 0,361 COS (1 ф,! + фф)] я« I (/со)!, (5.255)

Ф„У (со) = arctg фф 0,42 sin 2 (фф +1 ф, ). (5.256)

Независимость всех рассмотренных характеристик от амплитуды входного сигнала и послужила поводом для введения термина «псевдолинейное устройство».

Рис. 5.46. Примеры типовых л. а. х. ири псевдолинейной коррекции.

Для случая введения псевдолинейных корректирующих средств желаемые передаточные функции с заданным запасом устойчивости отличаются от тех, которые были рассмотрены в § 5.3. На рис. 5.46 приведены возможные типовые л. а. х. Пересечение оси нуля децибел происходит при наклоне асимптоты л. а. х. -40 дБ/дек. По сравнению с л. а. X. типа 2-1-2-3 и 1-2-1-2-3..., рассмотренными в § 5.3, здесь значительно подавлены высокие частоты, что позволяет получить лучшую фильтрацию помех (рис. 5.34). Непрерывная часть системы Е случае астатизма второго порядка (рис. 5.46, а) имеет передаточную функцию

WAP)=--. (5-257)

Амплитудный канал псевдолинейного корректирующего устройства содержит при этом звено с передаточной