B(t)\

из i

Ч(Р)

e(t)

%(P)

И32~

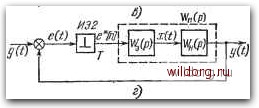Рис. 2.12. К определению передаточной функции импульсной системы

сделать только для г-преобразований или дискретных преобразований Лапласа входной и выходной величин, так как входная величина задана в виде решетчатой функции времени е\п\.

Можно ввести понятие идеального импульсного элемента второго рода НЭ2 (рис. 2.12, б), считая, что он генерирует с периодом Т последовательность бесконечно коротких импульсов типа б-функции, площадь которых пропорциональна сигналу ошибки е (t) в моменты времени

прикладываются затем ко входу звена с передаточной функцией Wb(p) Совокупность идеального импульсного элемента ИЭ1 и экстраполятора Э1 эквивалентна импульсному элементу.

Если поставить задачу отыскания передаточной функции экстраполятора Э1, то окажется, что это возможно

t = nT. Эту последовательность представим в виде

е*[п] = е (О 6{t-nT) = e {t) бг (0. (2.117)

где п = 0, 1, 2, ... Далее сигнал (2.117) поступает на экстраполятор Э2, который из импульсов типа б-функции формирует реальные импульсы заданной формы и продолжительности.

Представление импульсного элемента согласно (2.117) не соответствует действительности, так как никакой импульсный элемент не может генерировать бесконечные по высоте импульсы. Однако такое представление имеет свои преимущества. В этом случае может быть найдена передаточная функция экстраполятора Э2 в виде отношения непрерывных изображений Лапласа. Это связано с тем, что для каждого импульса типа б-функции, поступающего на экстраполятор, может быть найдено именно непрерывное изображение Лапласа, а не г-преобразование. Использование такой передаточной функции экстраполятора удобно вследствие того, что последующее звено с передаточной функцией W„{p) является непрерывным. Это облегчает изображение структурных схем.

Рассмотрим так называемую приведенную весовую функцию w„{f) разомкнутого канала управления (рис. 2.12, б). Под этим термином понимается реакция непрерывной части системы совместно с экстраполятором на единичную импульсную функцию е[п\ = Ьо[п\, которая дается формулой (2.45). Более строго приведенная весовая функция разомкнутого канала определяется как отношение выходного сигнала у {t) к высоте е единственного импульса ei6o[n] на входе экстраполятора (рис. 2.12, б):

wAt)=e-,y{t). (2.118)

Если выходную величину рассматривать только в дискретные моменты времени t = nT или t = {n-{- е) Т, то разомкнутый канал управления будет представлять собой импульсный фильтр. Он может характеризоваться решетчатой весовой функцией wln] или w„[n, е], полученной из производящей функции w„ (t).

Заметим, что приведенная весовая функция отличается от обычной весовой функции непрерывного фильтра как своим видом, так и размерностью. Приведенная весовая

lm=0

(2.120)

На основании формулы свертки (2.76)

Y{z)W{z)E{z), (2.121)

где дискретная передаточная функция W (z) есть г-преобразование от приведенной решетчатой весовой функции:

W {z) = S {wnW = wAnlz-". (2.122)

Последняя формула, вообще говоря, очевидна. Так как передаточная функция линейной системы не зависит от вида входного сигнала, то можно положить е [п] = = бо [п]. Изображение единичной решетчатой импульсной функции равно единице. Поэтому передаточная функция импульсного фильтра оказывается равной в этом случае изображению выходной величины, которая представляет собой решетчатую приведенную весовую функцию w„[n], и формула (2.122) может быть написана сразу.

В случае использования другого понятия идеального импульсного элемента в соответствии с рис. 2.12,6 и

функция содержит дополнительный множитель, имеющий размерность времени.

Знание решетчатой функции w„ [п] или w„ [п, е] позволяет найти реакцию импульсного фильтра на входную величину е[п] произвольного вида.

Очевидно, что реакция импульсного фильтра на дискрету е[0] будет tw„(0-e[0], реакция на дискрету е[1] будет ш„ {t - T)-e[l], реакция на дискрету е [т] будет Wa{t - тТ) х хе[т]. Поэтому

У(0== 2 e[m]w„{t-mT), Для дискретных моментов времени

4[п]= 2 e[m]wAn-m]. (2.П9)

m = 0

Найдем 2-преобразование от левой и правой частей последнего выражения: