соответствующее установившемуся состоянию, может сдвигаться в любую точку наклонной линеаризованной харак теристики, например в точку /. Это показано на рис. 6.19. Тогда возможные несимметричные режимы должны быть такими, чтобы среднее значение выходной величины было нулевым. Это правило и определяет требуемую точку сдвига начала отсчета на нелинейной характеристике при задании некоторого несимметричного режима. Дальнейший расчет, по сути дела, не отличается от случая расчета симметричных режимов. Здесь также следует проверить условие замыкания, как необходимое условие возможности существования подобного режима.

Во всех случаях расчета возможных симметричных и несимметричных режимов нет необходимости построения всей кривой Уо(0. как это показано на рис. 6.18 и 6.19. Доста точно, если будет найден периодический режим для дискретных точек t = nT, т. е. решетчатая функция Уо\п\. В соответствии с изложенным выше это может быть сделано точно по формуле (6.104). Возможное упрощение методики расчета заключается в том, что точным методом можно ограничиться при расчете прохождения периодического сигнала через дискретную часть канала (рис. 6.1). При нахождении периодического режима для выходного сигнала ЦВМ Хо\п\ нужно исходить из передаточной функции D{z), Тогда периодическая передаточная функция несимметричного вида (6.87) будет здесь равна

Рис. 6.19. Статическая характеристика входного преобразова-при наличии сдвига,

теля

Wm{z) = D{z)

(г - [у

(6.111)

В отличие от формулы (6.87), здесь г -число интеграторов в дискретной части системы, Qi (z) - полином, определяемый полюсами D(z), лежащими внутри круга единичного радиуса. Так как степень знаменателя D (z) может быть значительно ниже степени знаменателя W(z}, то расчеты здесь могут быть значительно более простыми.

Аналогичным образом может быть записана формула для Wkiz) и Wn{z).

После нахождения периодического режима на выходе ЦВМ может быть найден периодический режим на выходе экстраполятора Xi{t) без учета пока наличия вто- " " рого квантующего элемента (рис. 6.1).

В случае экстраполятора нулевого порядка это достигается фиксацией входной его величины на период дискретности и умножением на цену единицы младшего разряда выходного преобразователя. На рис. 6.20, а показан пример периодического режима Хо[п] на входе экстраполятора нулевого порядка, а на рис. 6.20, б - получающийся при этом периодический режим на его выходе. Для получения выходного сигнала экстраполятора первого порядка следует учесть, что его

дискретная передаточная функция для фиксированных точек i - nT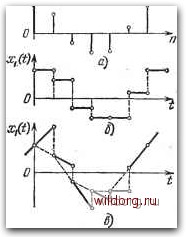

Рис. 6.20. Получение выходного сигнала акстраполятора.

г- 1\

= 1.

(6.112)

Поэтому значение выходной функции Xi{t) может быть найдено, если умножить дискреты сигнала на выходе ЦВМ на цену единицы младшего разряда выходного преобразователя, а затем провести прямые линии, соответствующие уравнению первого порядка, под углом, который определяется первой обратной разностью Vi [п]. Зто показано на рис. 6.20, в.

Найденная непрерывная периодическая функция Xi{t) действует на входе непрерывной части системы с передаточной функцией W„ (/;). Расчет периодического режима на выходе, т. е. нахождение непрерывной величины у (t), может быть сделан известными методами исследования

линейных непрерывных систем. В частности, можно разложить входную функцию Xi (t) па гармоники и найти выходной сигнал, удерживая в решении одну, две или более гормоник.

Учет влияния второго квантующего элемента. Выходной преобразователь К-Н -(рис. 6.1) может быть учтен в излагаемом методе расчета. Для этого необходимо пропустить через нелинейную характеристику преобразователя выходной сигнал ЦВМ.

Периодическая составляющая выходной величины преобразователя по аналогии с рис. 6.7, а может быть записана в виде

[n]={j-A + E {хЬ [п]}) б sign 4 [п]. (6.113)

Здесь xft [п] - периодическая составляющая выходной величины ЦВМ, Д -смещение начала отсчета относительно точки 2 (рис. 6.7, а), Е соответствует операции выделения целой части. В частном случае, тогда начало отсчета перемещается в точку 2, смещение Д = 0. Это соответствует симметричному периодическому режиму. Найденное значение л* [п] с учетом округления, вносимого вторым квантующим элементом, должно использоваться для нахождения сигнала на выходе экстраполятора (рис. 6.20).

Пример 6.3. Пусть в системе угловой стабилизации передаточная функция непрерывной части 1н(р)=нР, где ка = 40°/В. с, цена единицы младшего разряда входного преобразователя 6i=12 угл.мин, цена единицы младшего разряда выходного преобразователя 6 = 0,1 В, программа ЦВМ определяется передаточной функции

DA2) (1-а) г

где (3 = 0,92, период дискретности Г = 0,04 с. Определим возможные симметричные режимы, соответствующие случаю, изображенному на рис. 6.7, б. Рассмотрим периодический режим в виде прямоугольной волны (рис. 6.18, а), соответствующий условию для амплитуды колебаний О < Л < 6i. Изображение решетчатой функции на входе ЦВМ

«() =2 ?(1 + - +~""-