по первой, а по второй низкочастотной асимптоте желаемой л. а. X.), а i/Jj;--максимальное требуемое значение (/--1)-й производной управляемой величины с учетом требований по парированию возмущений.

Ограничение зоны нечувствительности. Для характеристики, изображенной на рис. 2.3, в, зона нечувствительности составляет 6i/2. Однако с учетом сказанного при построении этой характеристики (см. также рис. 2.3. г) зону нечувствительности следует принять равной ецбх. Подставляя последнее выражение в (6.116), можно получить условие для выбора основного числа разрядов выходного преобразователя при заданной его зоне нечувствительности:

«o3,3Ig(l-f). (6.117)

Необходимо отметить, что действительная зона нечувствительности в системе регулирования может отличаться от величины е„ за счет действия возмущений (например, нагрузочного момента от сил сухого трения в следящей системе воспроизведения угла).

Ограничение амплитуды периодических режимов. Если считать, что периодические режимы ограничены единицей младшего разряда входного преобразователя, то возможный симметричный периодический режим на входе ЦВМ будет иметь форму меандра (рис. 6.8). Тогда для амплитуды колебаний управляемой величины можно записать условие а < 0,5 6i. Это же условие будет иметь место и при несимметричном режиме. Однако действительная амплитуда колебаний может быть значительно меньше ее предельного значения 0,56i.

Для оценки ее величины можно воспользоваться следующим приближенным способом. При произвольном значении полупериода симметричных колебаний амплитуда первой гармоники входного сигнала

aisini. (6.118)

Амплитуда колебаний на выходе канала управления

ааг\ W* (/М 1 = f sin f\W* (j \. (6.119)

Здесь

%N(i>N = {Ni, 2, q) (6.120)

соответствует частотам возможных пгриодических режимов. Так, для рассмотренного примера 0.3 передаточная функция разомкнутой системы имела вид

6i (1-а) г 2 (г-1)2-Частотная передаточная функция

где постоянная времени

1-Ьа г 1-f 0,92 0,04 „ .„ = Т = Т=А92= 0.48 С.

Рассмотрим возможный периодический режим при N = 2. Тогда псевдочастота

В соответствии с (6.119) амплитуда колебаний на выходе

2-12 . .со 20 К 1-f 39,22-0,482 , asP«3-jsin45°--39ga---=1,33 угл. мин.

Полученный результат близок к тому, который был получен в § 6.3 точным расчетом. Однако для расчета по формуле (6.119) требуется знание относительного полупериода Л. Рассмотрим поэтому задачу определения амплитуды возможного периодического режима в несколько более общей постановке. Ограничимся случаем учета одного квантующего элемента и использованием типовых л. а. X. симметричного вида, которые были рассмотрены в § 5.4.

На рис. 6.22 построены типовые асимптотические л. а. X. симметричного вида. Кривая / соответствует статической системе, кривая 2 -системе с астатизмом первого порядка и кривая 5 -системе с астатизмом вто-

рого порядка. На том же рисунке изображена асимптотическая л. а. X., соответствующая множителю

(6.121)

при обобщении на случай, когда полупериод может быть дробным числом. Эта л. а. х. состоит из двух асимптот, одна из которых имеет наклон -f 20 дБ/дек и соответствует частотам 0<Я<2Г-1, когда синус может быть заменен углом, а вторая совпадает с осью нуля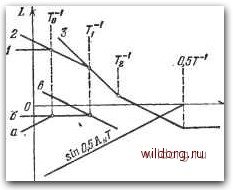

Рис. 6.22. К расчету амплитуд возможных нериодических режимов.

децибел и соответствует частотам 2Т~ < Я <; пТ-. Амплитуда первой гармоники колебаний пропорциональна сумме ординат двух л. а. х., соответствующих некоторой частоте солг N- Последнее равенство справедливо для частот о)л<27-1. Однако именно на этих частотах наблюдается наибольшая амплитуда колебаний.

На рис. 6.22 построены асимптотические л. а. х., соответствующие сумме ординат двух л. а. х. Кривая а соответствует статической системе, кривая б-астатизму первого порядка и кривая в -астатизму второго порядка. Из кривой а следует, что в статических системах наибольшие амплитуды автоколебаний будут наблюдаться в некотором интервале частот периодических или квазипериодических режимов. Этот интервал совпадает с интервалом частот, в котором проходит вторая асимптота