части канала управления

(3.258)

где Wio (г) - дискретная передаточная функция непрерывной части, включающей в себя звено с передаточной функцией Wta (р) и экстраполятор.

Из совокупности уравнений (3.226) - (3.256), в принципе, может быть определена зависимость =fi(av) после исключения неизвестных ё и F. В простейших случаях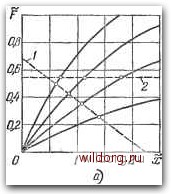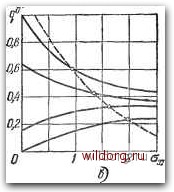

Рис, 3.29. Графики к определению X и Ох на входе нелинейного

звена.

ЭТО может быть сделано аналитически. В более сложных случаях -графическими построениями или расчетом на ЭВМ

Если ввести обозначения

TO уравнения (3.255)-(3.257) могут быть сведены к одному и представлены в виде

F{%, Ox) = t-

(3.259)

Графическое решение последнего уравнения показано на рис. 3.29, а. Пересечение наклонной прямой линии (прямая /), уравнение которой определяется формулой

(3.269), с исходным семейством характеристик F {%, Gje) дает отдельные точки зависимости x = fi(oJ.

Если регулярная составляющая g с течением времени возрастает по линейному закону, но ё = const, то, про-дифферерщировав (3.256) по времени, получим для производных

=F UmpWi {p) = ksF. (3.260)

При этом из условия ё = const следует, что limW„i(p) при р->-0 должен стремиться к бесконечности. Из (3.260) можно определить

F = J. (3.261)

где g = const - значение постоянной составляющей первой производной задающего воздействия. Если g возрастает по квадратичному закону, то из условия ё = const следует, что UmpWzip) при р-0 должен стремиться к бесконечности. Поэтому равенство (3.256) необходимо продифференцировать дважды. В результате можно найти

где &4 соответствует пределу, к которому стремится

FWaiip) при р-0, а g -значение постоянной составляющей второй производной задающего воздействия.

При известном значении F искомая зависимость может быть получена из того же семейства F {х, Gj,), если провести на нем горизонтальную прямую на уровне F. Это показано на рис. 3.29, а (прямая 2). Пересечение горизонтальной прямой с семейством F (х, о) дает отдельные точки искомой зависимости X = /i(o:).

Расчет прохождения случайной составляющей делается следующим образом. Спектральная плотность ошибки может быть записана в виде

St (К q) = ! UK q) Г S (К, (3.263)

где 5 (Я,) -спектральная плотность входного сигнала в функции псевдочастоты. Частотная передаточная

1 оо

1 + А Y

I +А 2

(3.265)

Частотная передаточная функция части канала управления от его входа до входа нелинейного звена определяется формулами

Wt UK е) = Wi (г, е). г=-f. (3.266)

11 (Z, е)=D (2)- (г, е), (3.267)

где Wiq{z, е) - дискретная передаточная функция части канала управления, включающей в себя непрерывное звено с передаточной функцией (р) и экстраполятор.

В уравнение (3.265) входят две неизвестные величины: X и Ох, так как коэффициент cf = q°{x, о)- В принципе это уравнение может быть решено и получена зависимость х=/2(Ол-)- В просгейших случаях эта задача может быть решена аналитически. В более сложных случаях возможно применение графических приемов, а также проведение расчетов на ЭВМ.

Для графического решения задачи целесообразно зависимость qO = q°(x, о) построить в функции Oj, для фиксированных значений х. Это показарю на рис. 3.29, б, где построена подобная зависимость при фиксированных значениях X.

После нахождения интеграла (3.265), что делается известными методами, будет получена зависимость о от эквивалентного коэффициента передачи 9". Задаваясь

функция для ошибки

Ht (А, cf) = [l + W* (А, cf>)]~ (3.264)

зависит также от эквивалентного коэффициента передачи q = q°(x. Ох). Дисперсия случайной составляющей на входе нелинейного звена может быть определена в соответствии с изложенным в § 3.9:

= \(Р) Р St (К ,0) а%

о -оо