Однако в главе 2 было показано, что частотные характеристики дискретных систем, построенных в функции абсолютной псевдочастоты К, для частот К <С 2Т- практически сливаются с частотными характеристиками непрерывной части. Поэтому можно воспользоваться известными приемами расчета последовательных корректирующих средств. Условием определения л. а. х. корректирующих средств (Х) = L>K (К) - L* (к) посредством вычитания из желаемой характеристики Lf,, (Я) располагаемой L* (к) является требование того, чтобы операции над частотными характеристиками производились в области частот k<i2T-. В этой области подобный метод оказывается практически точным, и он может использоваться.

При расчете непрерывных корректирующих средств импульсных И дискретных систем управления можно использовать частотные характеристики непрерывной части системы, построенные в функции обычной круговой частоты со. Если в результате такого расчета построена желаемая л. а. х. (ы) непрерывной части, то определение корректирующих средств можно осуществлять вычитанием = - L{(x>), где и L (со) соответствуют л. а. х. последовательного корректирующего устройства и ИСХОДНОЙ л. а. х. Этот метод является достаточно точным, и во многих случаях его использование является весьма удобным.

Пример 5.1. Произведем расчет системы с астатизмом первого порядка, с ЦВМ в контуре по следующим исходным данным: максимальная скорость входного воздействия gmax = 30 с , максимальное ускорение входного воздействия g„iax = 15 с~, максимальная допустимая ошибка воспроизведения входного сигнала етах = 0,1, допустимое значение показателя колебательности М = 1,5, период дискретности Г = 0,02 с, передаточная функция непрерывной части совместно с входным и выходным преобразователями имеет вид

" = Р(1+Т1Р)(1+Т2Р)(1+ТЗР)

где Ti = 0,05c, Та = 0,003 с, Тз = 0,001 с. В системе используется экстраполятор нулевого порядка. Требуется определить вид И параметры непрерывного последовательного корректирующего устройства, которое должно быть вве-

дено В канал регулирования, а также необходимое значение общего коэффициента усиления Ki-

На рис. 5.41 построены л. а. х. рассчитываемой системы. На рис. 5.41, а построена л. а. х. непрерывной части в функции круговой частоты to. На рис. 5.41,6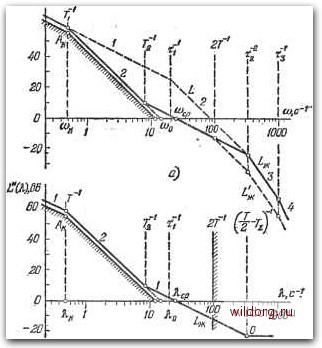

Рис. 4.41. Л. а. X. к расчетному примеру.

построена л. а. х. системы совместно с ЦВМ в функции

псевдочастоты = -tg-. Построенные л. а. х. L (со) и

L* (Я) совпадают в области низких частот, со < 2Т-, когда можно считать, что со?Я.

Запретная область для л. а. х. строится по условиям обеспечения требуемой точности. Построение ее аналогично при использовании частот со и Л. Ниже это

Постоянная времени корректирующего устройства, формирующая первый излом л. а. х., равна

Вторая постоянная времени (см. § 5.3)

Требуемое значение общего коэффициента усиления

д 30

/Cz = K2 1=1,41 = 420 с-\

•тах

Частота среза л. а. х.

420 0Л2.25.2С-

построение производится в функции псевдочастоты. Эквивалентная частота

Яе = = - = 0,5с-\ 6 max "

Базовая частота для запретной области

Желаемая асимптотическая л. а. х. в низкочастотной области формируется так, чтобы она проходила в точке излома выше контрольной точки Л> на 3 дБ. Она состоит ИЗ отрезков прямых с наклонами 1-2-1. Это дает желаемую частотную передаточную функцию в низкочастотной области

Параметры желаемой передаточной функции определяются следующим образом. Базовая частота л. а. х.