ШУМЫ КВАНТОВАЙИЙ

Фурье. Из формулы (3.179) имеем

eos4 + leos + icos+...

Использование этого разложения дает возможность представить формулу (3.182) в виде

КАР)-

2пЩ [ Т, + 4

.„ 4ят , 1 блт , \

°-ТГ+ 9-°-7Г+•••)• (3.184)

Во многих случаях для корреляционной функции (3.184) сравнительно просто может быть найдена спектральная плотность. Так, например, если на входе действует типовой входной процесс следящей системы [8] с корреляционной функцией для скорости Ki (т) = = of exp (- л I т I), то корреляционная функция помехи от квантования по уровню

/f,W-»-(cos + lco. + cos5+...).

Для этой функции нетрудно найти спектральную плотность (3.69):

5 (со).

ai =

bi =

(3.185)

Для случая, когда огибающая затухает медленно ()11<2лТс), корреляционная функция и спектральная плотность изображены на рис. 3.17. Корреляционная функция (рис. 3.17, aj получена из графика, изображенного на рис. 3.16, изменением периода и введением затухания по экспоненте с постоянной времени \.С. Спектральная плотность содержит ряд убывающих по высоте размытых пиков на частотах гармоник. Высоты пиков убывают пропорционально где / - порядок гармоники.

Для получения корреляционной функции решетчатого процесса следует в формуле (3.182) сделать подстановку

т = тГ, где Т -период дискретности. Тогда

К Am]

(3.186)

где А -целая часть относительного временного сдвига, определяемая выражением

(3.187)

Если использовать форму записи (3.184), то для дискретного процесса, описывающего шум квантования, корреляционная функция

6\К, [т]

2n=af

COS-

2лтГ

-bycos-yT-Ь ...

(3.188)

Рассмотрим теперь несколько случаев. Если скорость движения мала и Т<.Г, то при выполнении условия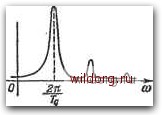

Рпс. 3.17. Корреляционная функция и спектральная плотность шума квантования для типового входного сигнала.

pT-l на основании (3.75) и (3.185) для рассматриваемого случая можно записать спектральную плотность в виде

" 2зх2 Ad Р \ \+ай-к+Ь,(П

1 = 1

Тс 1

i2n\

(3.189)

График спектральной плотности совпадает с изображенным на рис. 3.17,6 при замене частоты со на псевдочастоту Я. Если ограничиться учетом только первого

пика спектральной плотности, то ее можно записать в виде

1 \

N 1 +

I I 2А ,

(3.190)

Уровень спектральной плотности на нулевой частоте iV = S*(0) можно определить, интегрируя (3.190) в бесконечных пределах и приравнивая полученное значение дисперсии шума квантования D, = 6/12. В результате имеем

°6(.+Wr -

Случай очень медленного движения при выполнении условий 2я;Гс< и ТсТ следует исключить из рассмотрения, так как здесь не будет выполняться условие малого изменения скорости на интервале времени Т-

В случае медленного движения при Тс>Т, но при 2я;Тс>л спектральной плотности (3.190) на основании (3.75) соответствует корреляционная функция шума квантования

/H = --e-fi«icos. (3.192)

В случае быстрого движения, т. е. при выполнении условия ТТ, можно считать, что первый резонансный пик (рис. 3.17,6) сдвинут в область высоких частот, так что в полосе пропускания системы управления шум квантования будет белым с корреляционной функцией

/СЛ"]=4ИоИ = ОАИ (3.193)

и спектральной плотностью

St{k) = %-==N. (3.194)

Корреляционная функция (3.193) может быть получена из (3.188) при замене

(eosB-l-cosl-l-...)6o[m]. (3.195)