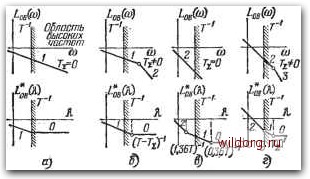Рис. 2.30. Высокочастотные части л. а. х. ЦАС е экстраполятором первого порядка.

Для случая, когда вертикальная прямая со=Т~ пересекается асимптотой л. а. х. W„(/co), имеющей наклон - 40 дБ/дек, передаточная функция в высокочастотной области представляется формулой (2.233) (при условии т = 0):

где Юов -базовая частота, определяемая (2.234).

Аналогичными рассуждениями можно показать, что дискретная передаточная функция в этом случае равна

1+1%{т-Ту)-(]гг{тт +

вительной сумме Tj;, тогда как в системах с экстраполятором нулевого порядка она равна Т+0,5Т.

Вместе с тем, как следует из (2.241), граница, разделяющая области низких и высоких частот, оказывается сдвинутой в сторону более низких частот и составляет со = Т~. Это поясняет рис. 2.30, на котором построены высокочастотные части л. а. х. при Т=0 (рис. 2.30, и) и при Tj:0 (рис. 2.30, б).

(2.247)

Полное выражение для дискретной частотной передаточной функции при наличии астатизма г-го порядка:

Фазовый сдвиг равен ар* (Я) = - г • 90° - 2 arctg Я +

+ arctg-\- Ц arctg Ятй- У arctg ЯГ,.

(2.248)

В районе частоты среза приближенное выражение для фазового сдвига может быть записано в виде

гп q

(Я) « - г 90° - arctg ЯГг + tg Ят - arctg ЯГ,.

fe=i i=\

(2.249)

Из уравнений (2.219) и (2.239) следует, что и в этом случае эквивалентная сумма малых постоянных времени составляет Г вместо значения Г+О.бГ, которое имело место в цифровых системах с экстраполятором нулевого порядка. Граничная частота, разделяющая области высоких и низких частот, также уменьшилась до значения со = Г-1.

В частном случае Г = О, что соответствует Г, = О (1 = 4-1, п), формула (2.246) приобретает вид

(i - А у) (1+А1.36Г) (1-А0,збГ)

. (2.250)

Этому случаю соответствует рис. 2.30, в. Другой случай, когда постоянная времени Гг достаточно велика и трехчлен в числителе (2.246) разлагается приближенно

у, (г-1) Т, sin

га-2гсо8-+1

на множители

1 + /X (т - Ts) - ijr (тт + 5) (I + АЛ (I - ATs),

изображен на рис. 2.30, г.

Не представляет труда распространить изложенную методику построения высокочастотной части логарифмической характеристики и на иные случаи пересечения прямой со = Т~* асимптотической л. а. х. непрерывной части.

Колебательные звенья. В непрерывной части канала управления может быть колебательное звено, передаточную функцию которого представим в виде

В частном случае при t, = 0 имеем консервативное звено.

Если выполняется условие Л 0,5 Т, то нахождение дискретной частотной передаточной функции не вызывает затруднений и может быть осуществлено в соответствии с изложенным выше при построении низкочастотной части.

При близости резонансной частоты колебательного звена 9j = T, к граничной частоте со = 2Т~, а также при выполнении условия qi>2T-* нахождение дискретной частотной передаточной функции имеет некоторые особенности.

Пусть для ЦАС с экстраполятором нулевого порядка в районе граничной частоты со = 2Г~ и в области больших частот передаточная функция непрерывной части с учетом преобразователей может быть представлена в виде

где соов -базовая частота (рис. 2.29). В частном случае, когда имеется звено без затухания ( = 0), дискретная передаточная функция в области высоких частот имеет вид

ЙОв (2) = -2 {р2 (I +rfp2) }