НЗ уровне U{)/tlmax

= 0,80 (прямая 2). Точки пересечения прямой 2 с исходным семейством кривых дают искомою зависимость x = /i(o:), или Xi = fx(ai).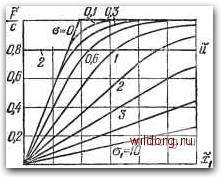

О 12 3

Рис. 3.32. К расчету первой зависимости к =

Далее проинтегрируем спектральную плотность S(A,) по всем частотам, что дает дисперсию

, да 2т -Т2 г

да2т 12 Т

Т \

фКт+1/

Нормированное значение среднеквадратичной величины

Рдг ! 1/ iL

1 ь б(2«-1) 2«-1 6Г

Фл:т+1/

Подстановка численных значений дает

2 2«

-1 К

0,004

2,38ф+Г

Эта зависимость построена на рис. 3.33 в виде штриховых линий для случаев а = 2, 3 и 4. На этом же графике нанесегю семейство кривых ср = ср (о) = ср (оJ6) при фиксированных значениях %i = xlb. Оно может быть получено перестройкой, например, графика, изображен-рюго на рис. 3.25, г. В данном случае оно было построено следующим образом. Представим эквивалентный коэффн-

4 5 <х=£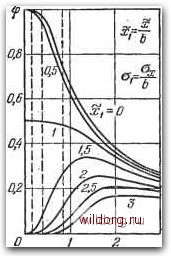

д б,

Рис. 3.33. К расчету второй зависимости X = /jCOjf).

(Х=2

Рис. 3.34. Определение математического ожидания и дисперсии на входе нелинейного звена.

циент передачи линейного звена с насыщением в виде

где в соответствии лой (3.251)

С форму-

ф(Х, Ох)=

1\ 6-jei\

+ Ф(

о, ySign(b-x)

Пересечение штриховых линий с исходным семейством кривых дает вторую искомую зависимость x = jf2(a:), или

Xl = /2(Ol)-

Полученные зависимости Xi=/i(o-i) и Xi = /2(ai) нанесены на общем графике (рис. 3.34). Они имеют точки пересечения j4i при а = 2, Л2 при а = 3 и Лз при а = 4. Точка Ац соответствует бесконечному числу разрядов выходного преобразователя (6i=0 и Oi = 0).

При а = 2 координаты точки Л] дают: %х = 1,375, х = frxi = 1,25.1,375= 1,58, 01 = 0,85, 0.= 1,25-0.85 = = 1,06. При трех разрядах получаем соответственно: JCi = 0,95, х=1,19, 01 = 0,36, 0J, = 0,45 - и при четырех разрядах: Xi = 0.85, х = 1,06,

1,5 01 = 0,17, 0 = 0,213.

По этим данным может быть произведен расчет ошибки ЦАС. Так как коэффициент передачи от входа си-

g g.io] " ПРОЦЕССЫ В ЗАМКНУТЫХ СИСТЕМАХ 243

стемы до входа нелинейного звена равен единице, то полученные значения х соответственно равны математическому ожиданию ошибки ё. Таким образом, при двух разрядах е=1,58, при трех ё=1,19 и при четырех ё=1,06. Эти цифры полезно сравнить с ошибкой при отсутствии влияния нелинейного звена, когда e=VlK=\. Таким образом, в рассматриваемой системе шум квантования во входных преобразователях увеличивает постоянное значение ошибки при движении с постоянной скоростью тем больше, чем меньше число разрядов в выходном преобр азователе.

Для расчета случайной составляющей необходимо по известным х тл определить эквивалентный коэффициент передачи ф или коэффициент (р. Это можно сделать, если воспользоваться приведенной выше формулой

Ч = Т

Подстановка в эту формулу полученных выше значений X Vi Ох дает для двухразрядного преобразователя Ф = 0,375, для трехразрядного (р = 0,547 и для четырехразрядного (р=0,808.

Далее в соответствии с формулой (3.269) имеем для спектральной плотности ошибки при /С" = (р/С

W*, КО)

1-f w*(A. <:)

Интегрирование этой спектральной плотности дает среднеквадратичное значение случайной составляющей ошибки 0,77; 0,36 и 0,18 соответственно для числа разрядов 2, 3 и 4.

Следует заметить, что в рассмотренном примере не учитывалась возможность существования периодических режимов, вызываемых квантованием по уровню (см. главу 6).