При повышенных требованиях, предъявляемых к системе в части ее точности, могут применяться л. а. х., в которых использован типовой «симметричный» переход оси нуля децибел (рис. 5.17). Подобная л. а. х. типа

О- 1-2- 1 -2... изображена на рис. 5.19. Она может быть образована из л. а. X. типа 2-1-2-3... (рис. 5.15, б) систем с астатизмом второго порядка или из л. а. X. типа 1- 2-1-2-3... (рис. 5.17) систем с астатизмом первого порядка.

Типовой асимптотической л. а. X., изображенной на рис. 5.19, соответствует передаточная функция разомкнутой системы

= (1+т,р) (1+Тхр) (f-b ia-f T)...(i+ТпР) (-

Базовая частота л. а. х. равна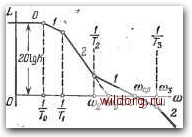

Рис. 5.19. «Симметричная» л. а. х. статической системы (тип О- 1-2 -1-2...).

(5.140)

При известных значениях То и базовая частота оказывается также известной. Тогда могут быть исполь-зовану формулы (5.113), (5.115), (5.121) и (5.122) для определения требуемого значения постоянной времени Тг и допустимой суммы постоянных времени Т. Эти формулы приобретают здесь вид

2 = il7w п

Т.ТгМ

K{M~l)

(5.141)

j VM (M - i) i M

tOo M +1 ~ M + 1

(5.142)

Т,ТгМ(М-1) K{M-\-l)

Учет некоторого дополнительного запаса устойчивости, даваемого отклонением л. а. х., изображенной на рис. 5.19, от л. а. X., систему с астатизмом второго порядка

т V т УМ(М-\) ( 1 1

1 = Ъ

м + \

К{м+1) К(м+1)-

В формулах для допустимой суммы постоянных времени (5.142) или (5.143) может также учитываться постоянное временное запаздывание т, имеющееся в канале управления.

Системы, содержащие колебательные звенья. В некоторых случаях объект управления представляет собой колебательное звено с передаточной функцией

o(P)=i+2gor!; + rgp- (5.144)

где 0 - безразмерный параметр затухания, Ог?о=1. а 9о = - угловая частота свободных колебаний. Иногда объекты регулирования, например гироплатформы, могут иметь более сложную передаточную функцию, но содержать также и подобное звено.

Колебательное звено, входящее в усилительный канал, сравнительно легко может быть учтено при формировании типовой л. а. X. в двух случаях: если его собственная частота колебаний значительно меньше частоты среза и если до значительно больше частоты среза. Рассмотрим эти случаи отдельно.

В случае низкочастотного колебательного звена практически только л. а. X. симметричного вида дает приемлемые результаты. На рис. 5.20 изображены л. а. х. и л. ф. X. статической системы, включающей в себя колебательное звено. Приведенной л. а. х. соответствует передаточная функция разомкнутой системы

(Р) =(1+2£оГоР + Г?Л (1 + Пр)0+Т,р)...{1 + ТпР) • - Для расчетов, связанных с получением требуемого запаса устойчивости, передаточная функция (5.145) может быть заменена эквивалентной функцией

(рис. 5.15) в области низких частот, изменяет формулу (5.142). В этом случае она имеет следующий вид [7]:

(Vm (М - 1) ( \ \ \ м

которая совпадает с (5.119). Значения добротности по ускорению и базовой частоты определяются выражениями

(5.147) (5.148)

Расчеты могут производиться в соответствии с формулами (5.113) и (5.120). Отличие фазовой характеристики (5.145) в низкочастотной области от фазовой характеристики (5.146), которая изображена на рис. 5.20 пунктиром, дает некоторый дополнительный запас устойчивости. Уточненная формула для допустимой суммы

Рис. 5.20. Л. а. X. и л. ф. х. статической системы с низкочастотным колебательным звеном.

постоянных времени Т, совпадает с (5.143), если заменить в ней (To + Ti) на 21,оТо-

При наличии высокочастотного колебательного звена, т. е. при выполнении условия - где Юо -

базовая частота, могут применяться л. а. х. любого типа как несимметричного, так и симметричного вида. Один из случаев изображен па рис. 5.21.

При выполнении условия оюо фазовый сдвиг, вносимый колебательным звеном в районе запретной зоны, можно принять равным - arctg 2оТо(й. Поэтому значение 2Со7"о должно входить в общую допустимую сумму постоянных времени Т, определяемую по одной из приведенных выше формул. Для того чтобы избежать появления второй запретной зоны для л. ф. х. в районе пика л. а. х.