Уравнение периодического режима (6.2) может быть записано в следующем виде:

1 +q* (ai, Фь N) W UnN) = О (6.3)

W (/JtyV-i) =

q* («1, (pi, N)

= -Z*(ab Фь yV). (6.4)

Частота периодического режима Q = nN~ находится Б целочисленном соотношении с частотой выдачи данных ЦВМ, равной 2пТ~. Это позволяет заранее знать все возможные частоты периодических режимов.

Обычный способ расчета периодических режимов заключается в совместном рассмотрении годографов комплексных величин W и - Z*. Точка пересечения для заданного значения N определяет амплитуду и фазу периодического решения. Это показано на рис. 6.3. Возможно использование и других методов расчета периодических режимов, например по кривой Михайлова.

Вместо частотной передаточной функции W при расчете периодических режимов может использоваться передаточная функция по псевдочастоте W* (/Я). Во многих случаях это оказывается более удобньш. Тогда вместо (6.3) и (6.4) будем иметь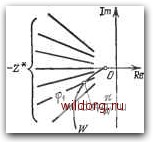

Рис. 6.3. К определению периодических режимов.

1 + 9*(«ь Ф1, yv)\r*(A)=o

(6.5)

W*(A) = -

- = -Z*(ai, ф1. Л/). (6.6)

д* (fli, ф1, N)

Псевдочастота К связана с круговой частотой ©i соот-

ношением

, 2 . шг 2 .

2N

(6.7)

При Л/=1 псевдочастота Я,->-оо, при N = 2, соответственно, К = 2Т-, при N3 приближенно можно положить, что я. я» со.

В соответствии с известной методикой определения периодических режимов [142] необходимо найти коэффициент гармонической линеаризации для нелинейной зависимости ео["]=/(е[п]), изображенной на рис. 6.2, с. В этом случае входной и выходной сигналы представляются в виде

У d,exp(jn). (6.8)

о[«]=4 2 б*ехр(/п), (6.9)

где dft и 6ft - комплексные амплитуды, l = N, если N нечетно, и l = N-l, если N четно. Комплексные амплитуды для входного сигнала определяются выражением

й,==а,е> = 2 4"]ехр(-/ v). (6.10) v=.o

Комплексные амплитуды для выходного сигнала в случае симметричной нелинейной характеристики определяются выражением

g, = b,,/*.=- 2 /(e[n])exp(-/v). (6.11)

Если N нечетно, то при k = N

N-i •

*=Ж 2 /(4«])exp(-/nv). (6.12)

Как следует из метода гармонической линеаризации, можно ограничиться в (6.9) учетом лишь первой гармоники, т. е. использовать гипотезу фильтра. Коэффициент гармонической линеаризации для первой гармоники

g*(Gi, Фь iV) = -e/№-i"). (6.13)

Обратная величина, взятая с обратным знаком,

-Z* (ci. ф1, iV) = -1 е . (6.14)

Для системы управления с ЦВМ определение периодических режимов при iV==l и iV = 2 может быть произведено ТОЧНО. Рассмотрим действующее на входе нелинейного преобразователя гармоническое воздействие

e[n] = alCOs(n-fфl) ( <ф1<У (6.15)

Здесь комплексная амплитуда di = Ci ехр (/фх). Для случая N=1 из формул (6.12) и (6.9) можно получить

во [п] =« bi cos лп, (6.16)

где bi = /(aiCos фх), а 6i=»»bi. Коэффициент гармонической линеаризации

9*= = ехр( М).

(6.17)

Для случая iV = 2 аналогичным образом из формул (6.11) и (6.9) можно получить

eo[n] = biCos(n-}-\pi). Комплексная амплитуда

6i = /Ф. = /(а1С08ф1)-}-/

GlCOS

(6.18)

(6.19)

Коэффициент гармонической линеаризации

9* = аГ =

/{а1С08ф1)-Ь/

Ol cos

п -l-n

(6.20)

При iV3 можно определить приближенное значение ео[п\, учитывая только первую гармонику:

(6.21)

Комплексная амплитуда

6,==М* = - 2 f(e[«l)ep(-/F)- (6.22)