Приведем геометрическую трактовку этого способа линеаризации. Изобразим графически зависимость F от xi при постоянных значениях всех остальных переменных:

л:2 = 4, 2 = 0, Хз = х1, Хз = Хз = Хз=0.

Пусть эта зависимость имеет вид кривой, представленной на рис. 2.2, а. Отметим значение х1 и проведем в точке С касательную. Тогда

/дР\о .

(2.6)

где ос -угол наклона касательной в точке С (л:?, F°), для которой Xi = xl и

F = F> = F{xl хЮ, х",. О, 0). (2.7)

Заметим, что, строго говоря, выражение (2.6) записано некорректно, так как справа находится безразмерная величина tgoc, а слева - величина, которая в общем случае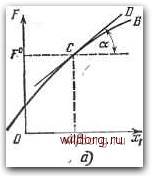

Рис. 2.2. Геометрический смысл линеаризации.

имеет некоторую физическую размерность. Более строго выражение (2.6) должно быть записано в виде

= tga.

(2.8)

где тр и mjc -масштабы величин F и ati, откладываемых на осях (рис. 2.1). Однако такая запись, вообще говоря, имеется в виду и в выражении (2.6).

Замена xi = лг? + Axi и сокращение члена (2.7), производившиеся раньше аналитически, здесь эквивалентны

переносу начала координат в точку С (рис. 2.2, а), в результате чего получается график рис. 2.2, б.

Первый член линейного уравнения (2.5) согласно (2.6) означает, что линеаризация уравнения геометрически может трактоваться как замена первоначальной кривой СВ на касательную к ней прямую CD. Из графика рис. 2.2, б очевидно, что эта замена тем точнее, чем меньшие величины отклонения Дхх возникают в исследуемом динамическом процессе (основная предпосылка для линеаризации); границы отклонений Axi, для которых допустима линеаризация, тем шире, чем ближе кривая СВ к прямой CD. Последним обстоятельством и определяются практически в каждой задаче те границы, внутри которых отклонения можно считать «достаточно малыми».

В ряде задач отличие от линейности, показанное на рис. 2.2, б, бывает столь незначительным, что даже в сравнительно большом диапазоне отклонений Axi можно считать систему линейной. В случае же ярко выраженной нелинейной зависимости линеаризации будет справедлива лишь на соответствующем более узком участке отклонений Axi.

Линеаризация в рассматриваемом смысле может быть совершенно недопустимой при скачкообразных зависимостях (релейные характеристики, сухое трение). Такого рода зависимости называются существенно нелинейными. Если по указанным причинам не может быть подвергнуто линеаризации уравнение только одного звена системы или даже только часть функции F для данного звена, то производят линеаризацию всех остальных нелинейных зависимостей, оставляя только одну или несколько существенно нелинейных.

Из приведенной геометрической иллюстрации вытекает второй способ линеаризации уравнений системы автоматического регулирования, который весьма часто применяется на практике. Этот способ заключается в том, что с самого начала все криволинейные зависимости, используемые при составлении уравнений звеньев, заменяются прямолинейными (по касательной в соответствующей точке кривой). Тогда уравнения звеньев сразу будут получаться линейными. Для упрощения записи значок Д перед переменными xi{t), Xi{t) и т. д. при этом опускается в предположении, что э,ти переменные представляют собой малые

отклонения от некоторого установившегося состояния и линеаризации уравнений уже проделана.

Применительно к цифровым системам управления описанный выше способ линеаризации может быть применен только к непрерывной их части. Распространить его на цифровую часть (ЦВМ с устройствами ввода и вывода) не представляется возможным.

Сама цифровая управляющая машина может реализовать как линейные, так и нелинейные закон управления. В последнем случае линеаризация не должна осуществляться при исследовании, так как при этом будет потерян весь смысл использования нелинейных законов управления.

Входные и выходные преобразователи (рис. 1.3) имеют статические характеристики ступенчатого (релейного) вида. Для подобных характеристик тангенс угла наклона либо равен нулю, либо стремится к бесконечности. Поэтому для входных и выходных преобразователей ЦВМ используется третий метод линеаризации. Он основан на предположении, обратном тому, которое принимается при линеаризации непрерывных систем. Если принять, что изменения входного сигнала по своей величине значительно больше единицы младшего разряда преобразователя, то можно пренебречь влиянием ступенчатости характеристики и линеаризовать ее, проведя некоторую «среднюю» прямую. Это поясняет рис. 2.3, а, на котором изображена начальная часть статической характеристики входного преобразователя (преобразователя непрерывной величины в код).

По оси абсцисс отложено непрерывное значение задающего воздействия g, а по оси ординат -его цифровое представление (число) go, получаемое на выходе входного преобразователя. Это число на рис. 2.3, а дано в десятичной системе счисления. Величина единицы младшего разряда на входе обозначена 6i. Эта единица младшего разряда имеет физическую размерность, совпадающую с размерностью задающего воздействия. Естественно, что единица младшего разряда на выходе преобразователя равна безразмерной единице.

В дальнейшем изложении будем предполагать, что протяженность всех горизонтальных площадок статической характеристики (рис. 2.3, а) одинакова и равна единице младшего разряда 8i. Это означает, что для характеристики