Функция, определяющая эквивалентный коэффициент передачи случайной составляющей, из формулы (3.219)

Аналогично из формулы (3.225)

Ф2 = g [Ф («i) + Ф (I «21) sign щ]. (3.251)

Здесь использованы обозначения, введенные ранее в формулы (3.244) -(3.246). Графики полученных зависимостей изображены на рис. 3.25, б, е и г.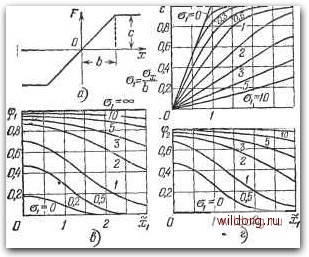

Рис. 3.25. Характеристики линейного звена с насыщением.

Кубическая характеристика. Зависимость вида F kx изображена на рис. 3.26, а. Из (3.215) имеем

Для случайной составляющей входного сигнала из (3.219) и (3.222), соответственно.

= --ф2(х, Ох).

(3.254)

Соответствующие графики построены на рис. 3.26, б, в. Пример 3.4. Рассмотрим разомкнутую цифровую систему, структурная схема которой изображена на

20 Ю

2 X/<3j; О

2 х/в

Рис. 3.26. Звено с характеристикой вида кубичной параболы.

рис 3.27. Примем, что на входе системы действует нормальный стационарный процесс с математическим ожиданием § = const и корреляционной функцией для центрированной составляющей /С (т) = ехр (-(хт1).

Нелинейное звено представляет собой реле с характеристикой, изображенной на рис. 3.24, а. Предполагается, что можно пренебречь влиянием квантования по уровню во входном и выходном преобразователях.

Передаточная функция непрерывной части

Дискретная передаточная функция приведенной непрерывной части

+ ТгР)

z-1 г - d

K{{\-d)z+d-d\ " z-d

где общий коэффициент усиления /C=6„6i, а d = ехр (- Т1Тг).

ЛСг)

±

Рис. 3.27. Схема к примеру расчета разомкнутой системы.

Дискретную передаточную функцию цифровой части примем в виде

п / \ I г-d

Результирующая дискретная передаточная функция канала

IW / \ r./\iv/ / ч к (l-d)z+d-d Wi{z, e) = D{z) Woi{z, S)=-Y:Zd- г -*

Частотная передаточная функция канала

i d+(l-2d+d)]K аК 6)= --f-

примем следунэщие исходные данные: постоянная составляющая §=5; дисперсия D„=100; коэффициент р = 2 с"; общий коэффициент усиления /С=1; ширина зоны нечувствительности реле Ь = 4 при т = 0,5; уровень сигнала на выходе реле с=20; постоянная времени Ti=0,5 с; период дискретности Г==1 с; <i = exp(-2) = 0,135.

Произведем расчет математического ожидания % на выходе линейной части. В соответствии с (3.205) имеем

V, ч /4iw / \ h к (\-d)z + d - d X (г, e) = G(z) Wi{z, б)=--f--.