
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [ 99 ] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] устойчивый предельный цикл. Убыванию X вдоль прямой L = О соответствует поворот прямой у = а - Хх вокруг состояния равновесия в точке перегиба характеристики у = ц){х). При Я = Яг прямая будет касаться характеристики в точке перегиба (L = О пересекает дискриминантную кривую в точке возврата) и возникнет сложное состояние равновесия, распадающееся при убывании X от значения Я = Яг на три простых: два неустойчивых узла (фокуса) и седло между ними. На интервале Яо < Я < Яг бифуркаций состояния равновесия не происходит. При Я = Яо оба фокуса становятся сложными, и при убывании Я от значения Я = Яо из них рождаются неустойчивые предельные циклы (первая фокусная величина «з положительна). Возникает структура фазового пространства с тремя предельными циклами, а-сепаратрисы седла идут к устойчивому циклу, охватывающему все три состояния равновесия, со-сепаратрисы скручиваются с неустойчивых циклов, охватывающих устойчивые фокусы. При дальнейшем убывании Я на интервале О < Яо < Яо смены устойчивости состояний равновесия не происходит, но при Я = О циклов уже нет (при Я = О существует интегральная прямая г/ = о, проходящая через все состояния равновесия). Предельные циклы могут исчезнуть, только превратившись в петли сепаратрис или слившись с циклами, вновь возникшими из петель сепаратрис. Существенно, что циклы вокруг фокусов и цикл, охватывающий все три состояния равновесия, имеют разную устойчивость. В соответствии со знаком седловой величины (гл. 11) только неустойчивые циклы, охватывающие состояния равновесия, могут превратиться (и обязательно превратятся при некотором Я = Я+) в петли сепаратрис. Эти две петли (возникающие одновременно, так как L = 0 - линия симметричных структур) можно рассматривать как одну вырожденную большую петлю, от которой при ее разрушении с убыванием Я возникает неустойчивый же предельный цикл, охватывающий три состояния равновесия. При некотором Я = Я* <Я+ предельные циклы, охватывающие три состояния равновесия, сливаются и при убывании Я исчезают. 3.4. Структуры разбиения фазового пространства и бифуркации при изменении параметров вдоль дискриминантной кривой. Проследим за бифуркациями и изменением структуры фазового пространства вдоль нижней ветви дискриминантной кривой, начиная от точки возврата (Я = я2). На интервале я1 <Я<я2 будет существовать структура с неустойчивым фокусом и седло-узлом G неустойчивой узловой областью внутри устойчивого предельного цикла (рис. 159,10). При убывании Я от значения Я=я1 фокус Xl меняет устойчивость и, так как аз > О, из него рождается неустойчивый предельный цикл (рис. 159,5). Чтобы проследить за дальнейшими бифуркациями при убывании Я до нуля, следует прежде всего выяснить структуру при ЯО. Она легко определяется, так как при Я = О существует интегральная пря- мая у = а, проходящая через оба состояния равновесия (устойчивый узел и седло-узел с устойчивой узловой областью). Предельных циклов нет. Качественная структура эквивалентна изображенной на рис. 159, i (узловая область покрыта штриховкой). 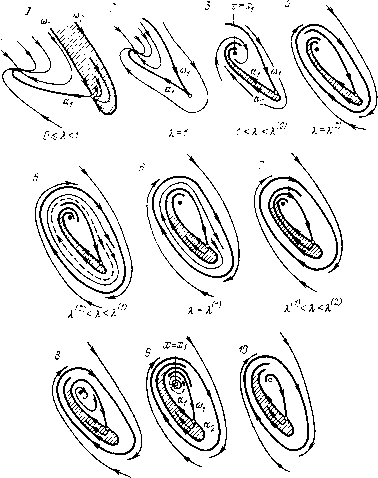 Рис. 159 Для седло-узла значение Я = 1 является бифуркационным. При Х< I узловая область устойчива (седло-узел имеет две ю-сепа-ратрисы coi и сог), при Я>1 неустойчива (седло-узел имеет две а-сепаратрисы ai и аг), при Я = 1 седло-узел вырождается (характеристическое уравнение имеет два нулевых корня) ) Проверка наличия или отсутствия предельных циклов для конкретной характеристики при А, == 1 может быть проведена численным счетом, например, траектории, проходящей через точку (хо, ф(а:о)) (ф(а:о) =-1). Предельный цикл, если он существует, находится в пределах прямоугольника с указанными в п. 3.2 свойствами. и узловая область исчезает (состояние равновесия имеет одну а- и одну со-сеператрису). Структура с сохранением типа состояний равновесия, как на рис. 159,1, осуществляется на интервале ОЖ 1. Для прослеживания бифуркаций вдоль дискриминантной кривой существенным является установление качественной структуры при Я = 1. Как будет видно из дальнейшего, при возрастании X от нуля необходимо возникает из сгущения траекторий двойной предельный цикл, охватывающий состояния равновесия, однако не существует способов обнаружить точные значения параметров, при которых он возникает. В дальнейшем будем предполагать, что при Я = 1 предельных циклов еще нет и осуществляется структура рис. 159, 2 (изменения в результатах, отвечающие предположению о существовании предельных циклов уже при Х = i, будут в дальнейшем указаны)). При возрастании X от значения Л = 1 возникает структура, качественно эквивалентная представленной на рис. 159,5. Возникает неустойчивая узловая область седло-узла (обе а-сепаратрисы выходят по направлению z = - 1, со-сепаратриса входит по на-правленпю х = - X). Узел становится фокусом при [1 - ср(xi)] - -4Ж0, где ф(х1) = (1/а)(&2-Зас-4аЯ). Сопоставим теперь расположение а- и ю-сепаратрис для структур на рис. 159, 9 и 159, 3. Отметим точки пересечения с а- и со-cenapaipncaMH на отрезке прямой х = xi выше фокуса (ближайшие по ходу сепаратрис от седло-узла). Для структуры на рис. 159,5 след ю-сепаратрисы па прямой х = xi расположен ниже следов а-сепаратрис. Для структуры на рис. 159,5, наоборо-рот - выше. При убывании X последовательно должны осуществиться бифуркации, соответствующие совпадению на прямой x = xi следа ю-сепаратрисы со следом ai-сепаратрисы (выходящей из седло-узла вверх) и со следом аг-сепаратрисы (выходящей вниз). Так как седловая величина {Рх + Qyjik-1 при Х> i положительна, то при образовании первой петли (при Х = Х) к ней стягивается неустойчивый предельный цикл (см. гл. И) (рпс. 159, 8). При расположении следа ю-сепаратрисы между следами аг и аг-сепаратрис будет существовать замкнутый контур, образованный ю-сепаратрисой седло-узла (рис. 159,7), При совпадении следов ю- и аг-сепаратрис при X = Я*" < Л возникает петля сепаратрисы (рис. 159,6), от которой при ее разрушении с уменьшением X рождается неустойчивый предельный цикл, охватывающий оба состояния равновесия, и возникает [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [ 99 ] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.0151 |