
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [ 105 ] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 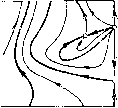 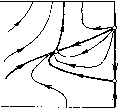 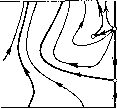 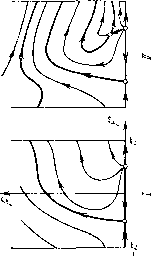 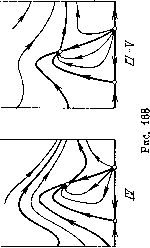 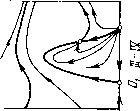 при возрастании р представлена па рис. 169. Для р = О картина разбиения фазового пространства па траектории представлена па рис. 169,1. 1) Предельных циклов пет, есть только две особые точки: 0\ - седло, о2 - неустойчивый узел. При достаточно малом изменении р число и характер особых точек не изменяются, но структура фазового пространства в целом изменится. В уравнении появится член -рр, и бесконечность станет неустойчивой. Из бесконечности появится устойчивый предельный цикл. Эта структура изображена па рис. 169, 2. 2) При возрастании параметра р точка в пространстве параметров попадает па кривую 1 + р - Я = О, и из сгущения траекторий возникает сложная особая точка седло-узел с неустойчивой узловой областью, изображенная па рис. 169, 2-3. При дальнейшем возрастании р сложная особая точка распадается па две простые: седло и неустойчивый узел (рис. 169,5). Следующая бифуркация прослеживается при переходе точки через кривую оз = 0; при этом из состояния равновесия при возрастании р появляется неустойчивый предельный цикл. Бифуркационному значению параметра р соответствует разбиение на траектории, представленное па рис. 169,5-4 (с особой точкой - сложным фокусом), а значениям справа от кривой оз = О (не слишком далеко от кривой)-картина, изображенная па рис.169,4. Вокруг устойчивого фокуса появился предельный цикл. Дальнейшие бифуркации при возрастании р будут бифуркациями сепаратрис. Проследим эти бифуркации. На прямой ф = arcsin Я", расположенной па полосе (-я, я) между точками Оз и О4 (па этой прямой сливаются точки Оз и О4, если 1 + р - Я = 0), отметим выше изоклины вертикальных па-клопов точки пересечения прямой с тремя сепаратрисами седла О4 и а-сепаратрисой седла 0\. Если параметр р взят достаточно близко к кривой Оз = О, то в порядке возрастания координаты р точки будут расположены в следующем порядке: Pi - па (о-се-паратрисе седла, Рг - па а-сепаратрисе седла, выходящей из седла влево, Рз - па а-сепаратрисе седла Oi и Р4 - па а-сепаратрисе седла, выходящей из седла вправо. При возрастании параметра р состояния равновесия Оз и О4 монотонно расходятся по неподвижной изоклине вертикальных наклонов: 5фз/5р = - рз(Ц- р2 - Я2)-/2 < о, 5ф4/5р = Р4 (1 + р2 Я2) -1/2 > О, а векторное поле по обе стороны изоклины поворачивается в противоположных направлениях: сверху - по часовой стрелке, снизу - против. Точки Pi, Рз и Р4 лежат па сепаратрисах, пе пересекающих изоклину вертикальных наклонов, и поэтому па прямой  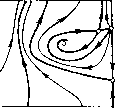 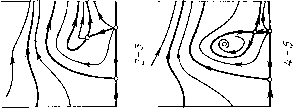 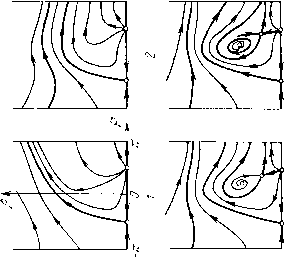 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [ 105 ] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.0091 |