При к = 3 ось h становится касательной к кривой »!;(/?, к) в точке /г = -2/3 (i;(-2/3, 3) = 0), и нри дальнейшем убывании А; от корня h = -2/3 отделяется корень, возрастающий с убыванием к. Этот корень с убыванием к продолжает дальше возрастать, проходит при к = Г* (-) через значение h = 0 ж затем

8л * /

становится положительным. При к = к* для положительного h == = h* оба положительных корня сливаются и при дальнейшем убывании к исчезают.

Отрицательные корни h = ho соответствуют неустойчивым предельным циклам, охватывающим состояние равновесия (так как, как легко убедиться, для них i. {ho, к)> 0).

Положительные корни соответствуют предельным циклам, охватывающим цилиндр. Легко убедиться, что меньший корень соответствует неустойчивому, а больший - устойчивому предельному циклу (это обстоятельство вполне наглядно отражено на рис. 153). Для меньшего корпя гз(/г, )>0, д.чя большего i,{h, к)< 0.

Корень /г = О соответствует влипапию предельного цикла в сепаратрису, идущую из седла в седло. При этом значении h происходит превращение цикла, охватывающего состояние равновесия, в предельный цикл, охватывающий цилиндр.

Слияние положительных корней при h = h* соответствует слиянию устойчивого и неустойчивого циклов в одпн полуустойчивый предельный цикл.

На основании проведенного рассмотрения мы можем сделать следующее заключение о возможной качественной структуре разбиения па траектории.

а) Состояния равновесия. При р О, по достаточно малом, состояния равновесия в точках (- л/2, 0) и (л/2, 0) остаются простыми седлами. Состояние равновесия в точке (О, 1) превращается в фокус - устойчивый, если к <3, неустойчивый, если к>3.

б) Поведение сепаратрис. Сепаратрисы, связанные с седлами в точках (-л/2, 0) и (л/2, 0), могут идти из седла в седло только прп зпачепии параметра к, соответствующем «влипапию» предельного цикла в сепаратрису; в других случаях сепаратрисы могут иметь своими предельными точками либо состояние равновесия (О, 1), либо предельные циклы, либо могут уходить в бесконечность. Поведение сепаратрис одиозиачио определяется характером и распределением циклоп.

в) Предельные циклы. Поведение предельных циклов определяется поведением корней функций ф(/г, к) в зависимости от к (папомпим, что k = XI\i, где К пропорциопальпо тяге пропеллера, ар - коэффициенту лобового сопротивления).

На рис. 154, 1-7 изображены возможные случаи разбиения фазового пространства па траекторип. Рис. 154,1 соответствует

случаю [1 = 0 (отсутствует лобовое сопротивление и тяга пропеллера). Последовательность рисунков от 2 до 7 соответствует последовательной смене качественных структур разбиения цилиндра на траектории при возрастании параметра к от нуля до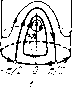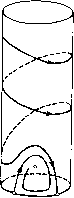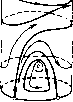

Рис. 154

сю (рис. 4а и 46 топологически эквивалентны; рис. 46 иллюстрирует превращение рис. 4а в рис. 5), т. е. при различных соотношениях между величиной силы тяги пропеллера и лобового сопротивления. Заметим еще, что все рисунки для наглядности даны со значительным количественным искажением масштаба. Точки + л/2 и - л/2 нарисованы схематично.

ГЛАВА 16

КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ПРИЕМОВ, ОПИРАЮЩИХСЯ НА ТЕОРИЮ БИФУРКАЦИЙ

§ 1. Квадратичное дифференциальное уравнение.

1. Оценки сверху числа предельных циклов, появляющихся при изменении коэффициентов из состояния равновесия типа фокуса или центра. Квадратичная система общего вида при наличии в начале координат фокуса или центра всегда может быть приведена к виду

x=--y + hx- Ux +{2X2 + Хь) ху + ХеУ, y=x + Xiy+ Хчх + (2Хз + Х)ху - Ху".

Решение вопроса о числе предельных циклов, появляющихся из состояния равновесия в системе (А), зависит от структуры коэффициентов функции последования в окрестности состояния равновесия и требует знания всех условий центра.

Полагая а; = р cos ф, г/ = р sin ф, переходим в системе (А) к полярным координатам и ищем решение системы в виде ряда по степеням начального значения ро. Отрезок прямой ф = О для всех достаточно малых р будет отрезком без контакта для траекторий системы. Полагая в найденном решении ф 2л, получим па некотором достаточно малом отрезке ф = О, О < ро < z функцию последования

р = PgMi (2л, + р1щ(2jx, яо + ...+p!;ufe(2jx, Я + ... (1)

Коэффициенты функции последования, как следует из их построения, есть целые функции параметров Я,, обращающиеся в однородные многочлены при Я] = 0. Для систем (А) известны все случаи центра (см. [147, 68*, 67*, 14*]), и они могут быть получены из условий обращения в нуль первых семи коэффициентов функции последования (трех последовательных ляпунов-ских величин):

«3 = - Яд (Яз - Яб),

«6 = 24 (3 - (4 + 5Яз - 5Яб),

"32

«7 = - 4 (3 - б) (36 - 2Х\ - Я).