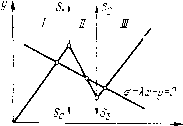Рис. 214

ветви характеристики, в области - падающий участок (рис. 214).

1. Состояния равновесия. Разбиение пространства параметров по числу и характеру состояний равновесия. Возможны одно и.яи три грубых состояния равновесия. В случае одного состояния равновесия имеем фокус (узел), всегда устойчивый в областях / или / и неустойчивый в области , если ос2>1. В случае трех состояний равновесия имеем

всегда устойчивые фокусы (узлы) в областях / и / и седло в области . Куски прямых о = XlK +

+ У1 и а = Х2к+У2 (Хи У\ и Х2,

У2 - координаты угловых точек характеристики) нри Ж осг образуют в плоскости (Я, о) дискримп-нантную кривую, отделяющую область трех состояний равновесия от области одного состояния равновесия. Точкам дискриминантной кривой соответствует сгиитое состояние равновесия типа седло-фокуса или седло-узла, и угловой точке (А, = ос2)-неустойчивый отрезок покоя, совпадающий с падающим участком характеристики.

В случае ос2 < 1 невозможны замкнутые траектории и возможными бифуркациями являются только ноявление и исчезновение состояний равновесия. Все нижеследующие рассмотрения ведутся для случая 0С2>1 и (oci - 1) < 4ос2, допускающего разнообразные бифуркации.

2. Бифуркации состояний равновесия.

2.1. Устойчивость состояния равновесия на линии сшивания. Пусть прямая а - Кх - уО проходит через угловую точку {х\, у\) характеристики на границе I ш II областей и пусть А, > (ос2 + 1)74 > «2. Тогда область / заполнена кусками траекторий устойчивого фокуса, а область - неустойчивого. Вводим на линии сшивания областей I и II положительные координаты и Si (а на линии сшивания областей и / - координаты 2 и з) (см. рис. 214). Преобразования Sq-Si по траекториям области / и 5] 0 по траекториям области запишутся так:

Si=Soexp{-hin[(Oi}, So = Si ехр{-h2n[(02}, (2)

где (Hi, -hi (j = l, 2)-мнимая и действительная части корней характеристического уравнения соответственно для областей I ш II.

Состоянием равновесия будет сшитый центр (5о = 5о), если hjdT + 2й2 =0> или, в раскрытом виде,

Я = Я+ = (aicca + 1) (а, - «2 + 2)"

Фокус на склейке будет устойчив {So<So) нри К Ж* и неустойчив {So> So) нри Я < Я"*".

2.2 Рождение предельного цикла из состояния равновесия типа фокус при перемещении состояния равновесия через линию сшивания. Докажем, что в областях I и II может существовать не более одного предельного цикла. Рассмотрим преобразование о-о по траекториям областей / и . Для области / будет

где бо - расстояние от границы раздела областей I и II jso состояния равновесия; % т 1 - монотонные функции (возрастающие или убывающие в зависимости от знака бо). Преобразование по траекториям области записывается аналогично. Вычисление производной функции последования дает

dSjdS„ = ЗД- ехр {- 2 {hx, + h}. (4)

Здесь т и Э - время движения соответственно по траекториям областей / и Я, Ai = (1 + ai)/2 > О, А2 = (1 - а2)/2 < 0.

Пусть состояние равновесия лежит в области /. Тогда для периодического решения {S = So) с увеличением о время Ti убывает (до значения л/coi), время 9 возрастает (до значения л/шг) и производная (4) растет. Поэтому может существовать не более двух точек пересечения функции последования с биссектрисой, причем неподвижная точка с меньшей координатой должна быть устойчива, а с большей - неустойчива. Так как, по предположению, состояние равновесия лежит в области / и является устойчивым фокусом, который не может охватываться устойчивым же циклом, то в областях I и II может существовать не более одного, причем неустойчивого цикла.

Пусть состояние равновесия лежит в области . Тогда с ростом 0 время Ti растет, а Э убывает. Аналогично находим, что в этом случае может существовать не более одного устойчивого предельного цикла.

Пусть о - Яж - г/ = О проходит через верхнюю угловую точку характеристики. Рассмотрим два случая.

1. Я>Я". Сшитый фокус устойчив. Траектория, проходящая через нижнюю угловую точку, в силу (2) при t-°o накручивается к состоянию равновесия. Эта траектория остается спиралью и при малых смещениях прямой а - кх - у = 0. Если при малом смещении состояние равновесия ионадает в область , то оно становится неустойчивым и, следовательно, появляется хотя бы один устойчивый предельный цикл. По сказанному выше этот цикл единственный. Пусть после смещения состояние равновесия

попадает в область /. Так как в объединении областей / и возможно существование не более одного цикла и фокус сохраняет устойчивость, то, следовательно, циклы не возникают.

2. Ж Х. Аналогично находим, что если при малом смещении состояние равновесия попадает в область , то циклы не возникают, а если в область /, то появляется неустойчивый цикл.

2.3. Рождение предельных циклов {простого или двойного) из границы области, заполненной замкнутыми траекториями. Рас-cinoTpuM преобразования So = f{So), склеенньхе из двух кусков: So = (f{So) - по траекториям областей / и и 5о = i]?(о) - по всем областям. Покажем, что f{So) дифференцируема в точке склейки. Преобразование Sq-S] но траекториям области / дано в (3). Преобразования S\j S2, 82- S3 и записываются анало-

гично. Значение dSo/dSo для функции ф(<5о) дано в (4), а для функции {So) будет

dSg/dS, = SgSo ехр {- 2h (т + Тд) - 2h, {г, + т,)}. (5)

Здесь Tl и тз - время движения по областям / и /, тг и Т4 - время движения по верху и низу области .

Пусть Sg = So- граничное значение, разделяющее интервалы определения преобразований ф(5о) и г)(5о). Производные для Ф и г) в точке склейки совпадают: при S = Sg будет тз = О, Э = 9*, T2+T4 = 9*.

Пусть теперь прямая а - Кх - у - О проходит через угловую точку характеристики xi, у\ и Я = Я. Покажем, что предельных циклов нет.

Функция последования на плоскости (о, о) склеена из отрезка биссектрисы 5д=5„<5о и кривой So - (So). Функция So = f{So) дифференцируема в точке склейки и, следовательно, нри Я = Я+ будет dSo/dSo=i (из (5) находим также, что d5„/dSo-<0). При возрастании от значения S* показатель экспоненты в (5) монотонно убывает от нулевого значения в точке склейкп (ti = const, тз растет и h\>0; тг и Т4 убывают и Л2<0). Других точек пересечения (или касания) с биссектрисой, кроме S = So, у кривой So = (So) быть не может. Кривая для •Sfl 0 располагается ниже биссектрисы. Спирали, сшитые пз траекторий в областях /, и /, накручиваются на границу области, заполненной замкнутыми кривыми, сшитыми из траекторий в областях I и II.

При малом изменении параметров а и Я функция последования измененной системы лежит в малой окрестности функции последования исходной системы. Если сдвигаться но полупрямой Li = 0 {Li = а - Kxi - yi, Я>ос2) от значения Я = Я"" в сторону уменьшения К, то функцией последования для S < S* будет прямая, проходящая через начало координат выше биссектрисы,