паратрисы на верхнем полуцилиндре образуют петлю, охватывающую цилиндр. Эта кривая будет однозначной по h для О < < 1 < 1, так как монотонному изменению h соответствует монотонный поворот векторного поля на верхнем по.туцилиндре. Бифуркационная кривая начинается в точке А = = 0.

При 1 = 1 на оси у = О - сложная особая точка седло-узел. Существует единственное значение h = ho, ири котором а- и со-сеиаратрисы седло-узла образуют петлю, охватывающую цилиндр. При О < h<ho существует устойчивый предельный цикл, охватывающий цилиндр; ири ho < h < оо все траектории имеют

Рис. 241

предельной точкой седло-узел. Циклов нет. Для > 1 при любых h существует единственный устойчивый предельный цикл, так как в этом случае нет особых точек, а бесконечность неустойчива (рис. 240, в).

Для уравнения (1) класс F{(f) может быть, например, расширен за счет полигональных характеристик (рис. 241, а)

f 2(ф-Ь л)/(л + Я) - 1, - л<ф<Я,, 1(ф) = \ 2(ф Шл-Я)-bl, К

Х)/{л - Х) + 1,

или характеристик релейного типа (рис. 241, б)

- л/{л + К), - л<ф<Я,, л/(л - X), Ж ф < л.

2(ф) =

Здесь X-«внутренний параметр» семейства характеристик.

Для этих характеристик легко найти уравнения кривых, на которых происходят бифуркации. Например, легко обнаружить, что при характеристике (7) бифуркационная кривая в плоскости ("(, h) проходит через начало координат и точку (1, 2У2/(л + в которой происходит смыкание с вертикальным куском границы.

Особенно простое уравнение бифуркационной кривой будет при Х = л (при этом характеристика (7) становится разрывной):

Y = -, Н =

При К¥=пш:<1-в фазовом пространстве па линии сшивания нет особых точек. Для x = л и y < 1 Две особые точки - фокус и (на линии сшивания) седло, сшитое из обыкновенных траекторий. Для у = 1 на линии сшивания сложная особая точка, исчезающая при y> 1-

При характеристике (8) смыкание бифуркационной кривой с вертикальным куском границы происходит в точке (y = = п/{л - Х), h = ho), где feo - корень уравнения

кЦп-Х)

1 - ехр

/1 (л - Я)2 (л + X).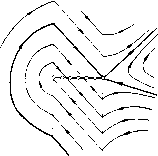

При y < л/(л - Я) в фазовом пространстве на линиях сшивания две особые точки, сшитые из обыкновенных траекторий: сшитый фокус и сшитое седло. При = п/{п - X) возникает особое образование (рис. 242), сходное с седло-узлом, содержащее отрезок Рис. 242

притяжения г/ = 0, /\,<ф<яи исчезающее при возрастании y (индекс замкнутой кривой, содержащей внутри отрезок притяжения с примыкающими к нему траекториями, равен нулю).

Пространство параметров (y, h) уравнения (1) будет грубым по отношению к классу характеристик F{((i), Fi((p) и /2(ф), если отождествить в указанном выше смысле сходные элементы притяжения или отталкивания.

§ 5. Динамическая система, описывающая автоколебания синхронного мотора. Приведем некоторые примеры систем с более сложным разбиением пространства параметров - грубым по отношению к некоторому классу характеристик. Рассмотрим систему (уравнения автоколебаний синхронного мотора) (гл. 18, § 3)

dy/dt = D-Wi{(p)-[A+BW2{(f>)-CWii)]y, d(f/dt = y, (9)

где Ч1(ф) (нечетная) и 2{(р) (четная)-периодические с периодами соответственно 2л и л, для трех видов характеристик: аналитической Ч"1=8тф, Чг = cos 2ф (рис. 243, а), полигональной (рис. 243, б) и релейной (рис. 243, в).

Введем малый положительный параметр р, положив D = pf, а = \ьа, 5 = рР, с = py- Для аналитических характеристик получим уравнения

dy/dt = - sin ф -Ь р [г - (а -Ь р cos 2ф - Y sin (f)y], d(f/dt = у. (10)

Система (10) имеет два состояния равновесия: фокус и седло. При малых р, фокус будет устойчивый, если а + > О, и неустойчивый, если а + Р < 0.

Структура разбиения фазового пространства на траектории определяется характером особых точек, характером и расположением предельных циклов и поведением сепаратрис. Мы рассмотрим эту систему методом Понтрягина (см. гл. 15).

4. *

Рис. 243

При р, = О система (10) имеет интеграл Н{<f, у) уУ2 - - cos ф = А. Значениям константы h из интервала -1 < й < 1 соответствуют замкнутые интегральные кривые, охватывающие состояние равновесия (типа центр), значениям из интервала 1 < А < оо - охватывающие фазовый цилиндр. При й = 1 сепаратрисы седла образуют петлю, охватывающую цилиндр.

Если систему (10) записать в виде

d(pldt = Ну + ]ip{cp,y), dy/dt =-Н + yiq{(p,y), (11>

то значения константы h, выделяющие кривые консервативной системы, вблизи которых при малом на верхнем и нижнем полуцилиндрах будут предельные циклы системы (И), соответственно определяются как корни уравнений

bih)=0, a32(/i)=0,

lfl (А) = j qd(p - pdy = [Г - (а + Р cos 2ф - Y sin ф) у] d(f =

2Я

Р J [v - (о - 2 sin" ф) /2(cos ф +h)] dtp