состоянию равновесия или предельному циклу, к которому стремилась а-сепаратриса седла. При обратном изменении к имеет место необратимость (изображаюпая точка, находящаяся около устойчивого состояния равновесия или предельного цикла, к которому стремилась указанная а-сепаратриса седла, не реагирует на образование петли сепаратрисы).

Мы остановимся сейчас еще на весьма интересных случаях, связанных с опасной границей, возникающей при существовании сложного фокуса и двукратного цикла, в которых не! можем однозначно указать поведение системы после прохождения через границу области Рауса - Гурвица.

Предположим, что неустойчивый предельный цикл, на который навивается при t - <» несколько сепаратрис, входящих в границы ячеек с различными центрами притяжения, устойчивыми состояниями равновесия или предельными циклами (рис. 123,а), при возрастании параметра стягивается к устойчивому фокусу, в окрестности которого находилась изображающая точка. Пусть при Я = Яо (рис. 123, б) предельный цикл влипает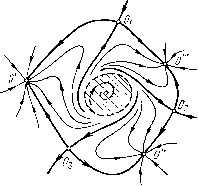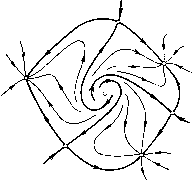

Рис. 123

в состояние равновесия, которое делается сложным неустойчивым фокусом, а затем грубым неустойчивым фокусом. При Я > Яо сепаратрисы стремятся к этому фокусу, и, очевидно, нет возможности однозначно указать, к центру притяжения какой из ячеек (для всех этих ячеек фокус является теперь граничным) будет стремиться изображающая точка (см. [141])).

Полностью аналогичная ситуация имеет место также, например, в случае, когда изображающая точка двигается по

") Таким образом, можно сказать, что мы имеем здесь «динамическую неопределенность».

устойчивому предельному циклу Lq, внутри которого находится единственное неустойчивое состояние равновесия типа узел или фокус.

К циклу Lq приближается неустойчивый предельный цикл L, являюгцийся предельным для ряда сепаратрис, входящих в границы ячеек с различными центрами притяжения. При некотором значении параметра % = ко цикл Li сливается с циклом Lq и исчезает.

В рассматриваемом случае, так же как и в предыдущем, нет возможности однозначно указать поведение изображающей точки при К > Ко.

ЧАСТЬ III

КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ КОНКРЕТНЫХ ДИНАМИЧЕСКИХ СИСТЕМ С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ

ГЛАВА 14

ОБЩИЕ ЗАМЕЧАНИЯ О ПРИЕМАХ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ

Введение. В настоящей части приводятся примеры качественного исследования динамических систем из приложений, в той или другой форме опирающиеся на изложенные в ч. I классические приемы качественного исследования (метод малого параметра, установление характера состояний равновесия, критерии Бендиксона и Дюлака, построение топографической системы, использование теории индексов) и на приемы, использующие теорию бифуркаций.

В книге особое внимание уделяется именно использованию методов теории бифуркаций.

Сделаем прежде всего некоторые общие замечания.

Мы уже говорили, что одной из наиболее трудных задач качественного исследования динамической системы является задача установления существования или отсутствия предельных циклов. При этом мы останавливались (см. § 13 гл. 1) на том элементарном факте, что по локальным свойствам разбиения на траектории ничего нельзя сказать о существовании или отсутствии замкнутой траектории.

Иногда в литературе встречаются работы, в которых делаются попытки дать общий универсальный алгоритмический метод отыскания предельных циклов для любых динамических систем с аналитическими (или неаналитическими) правыми частями.

Постараемся пояснить бессмысленность таких попыток на простом примере. Предположим, что рассматриваются всевозможные аналитические на некотором промежутке значений х функции y = fix) и ставится вопрос об общем универсальном методе отыскания (разделения) корней любой из функций

/о()=0.

Предположим, что рассматриваются функции f{x), аналита ческпе при всех х (-°° < х < +°о), и ставится вопрос об общем универсальном методе определения числа корней любой из этих функций /о(а;)=0 на некотором конечном интервале значений х