
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [ 22 ] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] Эти уравнения дают для рц, р\2, Р2\, Р22 решения, не равные тождественно нулю, только в том случае, когда A,i и К2 являются корнями уравнения а~1 Ь = А,2 - (а + d) X + (ad - Ъс) = О, (4) с d - А, которое называется характеристическим. Корни Я1 и А,2 называются характеристическими корнями состояния равновесия (особой точки). Рассмотрим различные случаи, которые здесь могут представиться. 1. Корни А,1 и А,2 действительны и различны. Тогда из урав-нений (3) можно найти рп, Р12, Р21, Р22 такие, что =70, Р21 Р22 И, следовательно, приведение динамической системы (А) к виду (2) возможно. 2. Корни А,1 и А,2 кратные, A,i = А,2 = А,. В этом случае приведение к виду (2), вообш,е говоря, невозможно. Однако в этом случае можно указать неособые преобразования, с помогцью которых система приводится к виду du/dt = Хи + . .dv/dt = Kv + ци + ... (5) (В частных случаях ц, может быть равно нулю.) Этот вид называется каноническим в случае кратных корней. 3. Корни А,1 и Я2- комплексные сопряженные: Xi - а + i, А,2 = а - ф (Р О, а может как быть, так и не быть равным нулю). В этом случае при действительных и т) мы получим комплексные сопряженные и ж v, так что приведение к виду (2) невозможно. В этом случае, вводя новые переменные ui, vi, и = = ui + ivi, V = u\ - ivi, нетрудно установить, что система может быть приведена к следуюш,ему виду: du\/dt = aui - fiVi + .. dvi/dt = ui + avi -t-..., (6) который в этом случае считается каноническим видом. Дополнительно отметим, что если рассмотреть линейную систему dl/dt = al + Ьт), dц/dt = с + d, которая получается из системы (А) отбрасыванием нелинейных членов, то, как известно, обш,ее решение этой системы имеет вид I = q е + Cj е, ц = CjXe-* + cJ". Здесь А,1 и А,2 являются корнями того же характеристического уравнения (4). Характеристические корни не меняются при линейной замене координат (характеристические кор-5» = 0, § 3. Возможный характер простых состояний равновесия. Грубые состояния равновесия. Сохраняем обозначения Характеристическое уравнение (4), очевидно, может быть записано в виде Я - оЯ -Ь А = 0. Возможны следующие случаи. I. Д > О, o - 4А > О, корни характеристического уравнения действительны и одинаковых знаков. В этом случае все траектории, проходящие через некоторую достаточно малую окрестность состояния равновесия О, стремятся к О: при t -t-oo, когда Я] и Яг отрицательны, при -°°, когда Я1 и Яг положительны). Состояние равновесия называется устойчивым узлом, когда Я] < О, Яг < О, и неустойчивым узлом, когда Я1 > О, Яг > 0. II. Д < О, корни характеристического уравнения действительны и различных знаков: Я1Я2 < 0. Состояние равновесия является седлом. III. Д>0, o -4А<0, 0=0, корни характеристического уравнения комплексные сопряженные: Я1 = а -f ф, Яг = а - причем действительные части этих корней отличны от нуля.
и элементарных предложений линейной алгебры. ) Напомним (см. гл. 1), что изображающая точка не может стремиться к состоянию равновесия при t, стремящемся к конечному значению. ни ЯВЛЯЮТСЯ инвариантами линейного преобразования координат), т. е. пусть дана система dxMt = ах + by + ..., dy/dt = сх + dy + ..., у которой характеристические корни Х\ и Яг. Пусть после линейного преобразования X = qnu + qizv, у = q2iu + q22V мы получаем систему в новых координатах и ж v du/dt = Аи + Bv + ..., dv/dt = Cu + Dv + ... Тогда характеристические корни последней системы, т. е. корни характеристического уравнения A-l В С D-% равны Я] и Яг). В ЭТОМ случае (так же, как и в случае I) все траектории, проходящие через некоторую достаточно малую окрестность состояния равновесия О, стремятся к состоянию равновесия О: при f + оо, когда а < О, при t - °°, когда а > 0. Состояние равновесия называется фокусом и при этом устойчивым, когда а<0, и неустойчивым, когда а>0. § 4. Замечания о методах установления характера грубых состояний равновесия. Указанный в предыдущем параграфе характер состояний равновесия в случаях I-III может быть установлен различными методами. В случаях I и III (узел и фокус) качественная структура состояния равновесия может быть установлена, если заметить, что в окрестности этих состояний равновесия окружности (или в случае III - эллипсы) являются циклами без контакта, которые все траектории пересекают, входя внутрь при ?и < О, < О я а < О (рис. 37, а, б) (или выходя из них при ?и > О, > О и
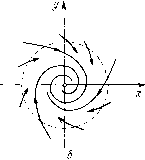 Рис. 37 а > 0). При этом узел или фокус имеют одинаковую качественную структуру в смысле введенного в § 14 гл. 1 определения» Качественный характер состояния равновесия в случае II (седло) может быть установлен с помощью естественного выделения в окрестности этого состояния равновесия дуг без контакта, изображенных на рис. 38. Непосредственное рассмотрение поведения траекторий при наличии таких дуг без контакта с последующим доказательством единственности в каждом из треугольников «разделяющей» (сепаратрисы) полностью устанавливает качественно характер состояния равновесия в этом случае [12, ISIJ, Сведения о других методах исследования состояний равновесия в случаях I-III можно получить в [12] (где указана и соответствующая литература). См. также [116-118], [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [ 22 ] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.0124 |