Т. е. контакт ложный - траектории системы (1) при КФО образуют с траекториями консервативной системы угол одного знака.

Заметим, что для двух различных значений параметра К: ki и Яг, траектории системы с Я = Я] пересекают повсюду траектории системы с Я = Яг.

Направление поворота векторного поля определяется знаком я1 - Яг, что следует из рассмотрения контактной кривой системы с Я == я1 и системы с Я = Яг:

{dyldx)x=% - {dy/dx)f-x = Я1 - Я.

Кроме того, как мы видели, при фиксированном значении параметра р при всех Я =5 О начало координат - фокус или узел, точка 0)- седло, и положение п характер состояний равновесия на экваторе не меняются.

Разбиение сферы Пуанкаре на траектории при значениях параметра р<0, р = 0 и р = 1 сохраняет свою качественную структуру при любых значениях Я > 0.

В случаях 0<р<1 и р>1 качественная картина разбиения сферы Пуанкаре на траектории зависит от величины параметра Я (см. подстрочное примечание на с. 126).

Рассмотрим случай 0<р<1. При Я = 0 имеет место рис.82 гл. 6.

При Я > О поведение сепаратрис седла S, попадающих внутрь областей ASM, MSN, NSB, ограниченных сепаратрисами консервативной системы и дугами экватора (эти области не содержат особых точек, лежащих в конечной части плоскости), в силу поворота поля определяется однозначно (см. рис. 87 гл. 6). Поведение уса седла, попадающего в область G, ограниченную сепаратрисами SA и SB консервативной системы и дугой экватора и содержащую внутри себя особую точку, не определяется однозначно и зависит от параметра Я.

Есть три возможности для поведения этого уса седла:

а) идет в узел (В) на экваторе;

б) идет в сложную особую точку Q (седло-узел) на экваторе;

в) идет в особую точку К (фокус или узел) внутри области G.

Вторая возможность имеет место при значении параметра Яо=(1-[г)/П1.

В этом случае существует интегральная прямая, идущая из седла в особую точку Q (седло-узел) на экваторе. Уравнение интегральной прямой будет

у = 1ц{х- 1/р),

что непосредственно проверяется. Качественная структура разбиения сферы Пуанкаре на траектории определяется теперь од-

нозначно и изображена на рис. 124. Значение параметра К = Ко, очевидно, бифуркационное. При КЖо качественная картина будет иметь вид такой же, как на рис. 88 гл. 6, а при К < Ко будет иметь место рис.87 гл. 6. Во всех случаях структура определяется однозначно.

Рассмотрим случай р->1. При К = 0 имеем качественную картину, изображенную на рис. 84 гл. 6. При К> О однозначно определяется поведение смещенных сепаратрис, попадающих в

Csm узел

Седло-узел

Сейло

Csdno узел

Устойчивый Фанус \ эзеп (узел)

Рис. 124

Седло-узе/1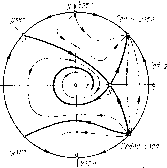

Седло-

УстоичиЗыи фонде

Рис. 125

области I-III (область / ограничена сепаратрисами SM и SN консервативной системы и близлежащей дугой экватора, область заполнена замкнутыми кривыми, область / ограничена сепаратрисами SN и ST консервативной системы, отрезком RT оси X и дугой PQN, включающей дугу экватора). Они ведут себя так же, как при малых значениях К.

Поведение сепаратрисы, входящей в область IV (симметричную области / относительно оси х), не определяется однозначно и зависит от величины К (аналогично случаю О < р, < 1 здесь имеется три возможности).

1) При Ко = {ц- 1)/ Ун существует интегральная прямая

у = -Уц{х- 1/р,),

идущая из седла S в седло-узел Р на экваторе сферы Пуанкаре-качественная картина изображена на рис. 125; Яд = (р,- -1)/Vp, - бифуркационное значение.

2) При А, > Яо и Я < Яд поведение сепаратрисы определяется однозначно, и соответственно имеем качественные картины, изображенные на рис. 88, 89 гл. 6.

На рис. 126 представлено разбиение пространства параметров Я, Ц. Точкам на осях Я и р,, а также на кривой р-Я - (р, - 1) = О соответствуют бифуркационные структуры.

3) При Я, = 0 на фазовой плоскости {х, у) существуют области, заполненные замкнутыми кривыми, при цК - {ц - 1) = 0 существуют сепаратрисы, идущие из седла в седло (интегральные прямые), и при р = О - сложная особая точка высокого порядка, распадающаяся при изменении параметра р.

Пример 2 [30].

dx/dt = ах+ by - х{х + у), dy/dt cx + dy - y{x + у).

Особые точки фазовой плоскости удовлетворяют системе уравнений

ах + Ьу-х{х + у)=0,

Рис. 126

сх + dy - у (х + у) = 0.

Умножая первое из этих уравнений на у, второе на а; и вычитая, получим следующее уравнение, которому должны удовлетворять координаты особых точек:

аху + by - сх - dxy - 0.

Полагая у = кх, мы получаем уравнение для к

bk + (a-d)k-c = 0. Корни этого уравнения действительны в случае, когда

D={a-d) + Abc>0.

Обозначаем их через ki и /сг и, подставляя в одно из уравнений (3), получаем в этом случае пять состояний равновесия:

х = 0, у = 0; x=±f-

Ьк,

у = ±к,

1 + 1

+ Ък

Состояние равновесия а; = О, г/ = О, очевидно, простое, если А = ad-ЪсФО). Нетрудно также видеть, что в случае Д > О остальные состояния равновесия тоже простые. Отметим, кроме того, что при D > О прямые у = kiX {i = 1, 2) являются интегральными прямыми рассматриваемого дифференциального уравнения, так как соотношение

cx + dy - y {х + у)

ах-\-Ъу - X {х + у)